8 bài học về học tập suốt đời từ một nhà vật lý thiên văn

Ngoài các ngôi sao, thiên hà, và lực hấp dẫn, việc nghiên cứu cách hoạt động cơ bản của tự nhiên tiết lộ những bài học có thể áp dụng rộng rãi cho những người học ở khắp mọi nơi.

Mở đầu

Mặc dù hầu hết chúng ta đều bị cuốn hút bởi vật lý thiên văn – ngành khoa học nghiên cứu những gì hình thành tự nhiên trên toàn vũ trụ – nhưng rất ít người thực sự chọn con đường trở thành một nhà vật lý thiên văn.

Để đạt được điều đó, một người không chỉ cần nắm vững nhiều công cụ toán học mà còn phải học cách tìm ra giải pháp khi đối mặt với những vấn đề khó khăn. Đôi khi, chúng ta gặp phải những giới hạn cơ bản:

– Giới hạn về dữ liệu hoặc thông tin có thể thu thập được,

– Giới hạn trong khả năng áp dụng lý thuyết của chúng ta,

– Hoặc thậm chí giới hạn về việc giải quyết vấn đề, ngay cả khi xét trên nguyên tắc.

Là những nhà vật lý, chúng ta không thể kiểm soát hay quy định các quy luật của tự nhiên; chúng ta chỉ có thể cố gắng mô phỏng thực tế một cách gần đúng nhất trong nỗ lực mô tả tự nhiên.

Dù vậy, có một tập hợp các kỹ năng cụ thể mà một người phải phát triển để trở nên thành thạo trong lĩnh vực vật lý thiên văn.

Trong khi nhiều người lo lắng về độ khó của toán học cần thiết để giải quyết những vấn đề này – từ đại số, giải tích, phương trình vi phân cho đến những chủ đề phức tạp hơn – thì thực tế, kỹ năng toán học có thể được luyện tập và cải thiện giống như bất kỳ kỹ năng nào khác: vẽ tranh, bơi lội hoặc chơi piano. Nếu bạn muốn giỏi vẽ tranh, bạn phải vẽ; nếu bạn muốn giỏi bơi, bạn phải bơi; và nếu bạn muốn giỏi giải toán, bạn chỉ cần luyện tập giải chúng.

Tuy nhiên, trên hành trình trở thành một nhà vật lý thiên văn, đặc biệt là khi bạn đã có được những kỹ năng cần thiết, một loạt các hiểu biết sâu sắc hơn sẽ xuất hiện. Dưới đây là tám bài học quan trọng áp dụng gần như phổ quát cho những người học tập suốt đời ở khắp nơi.

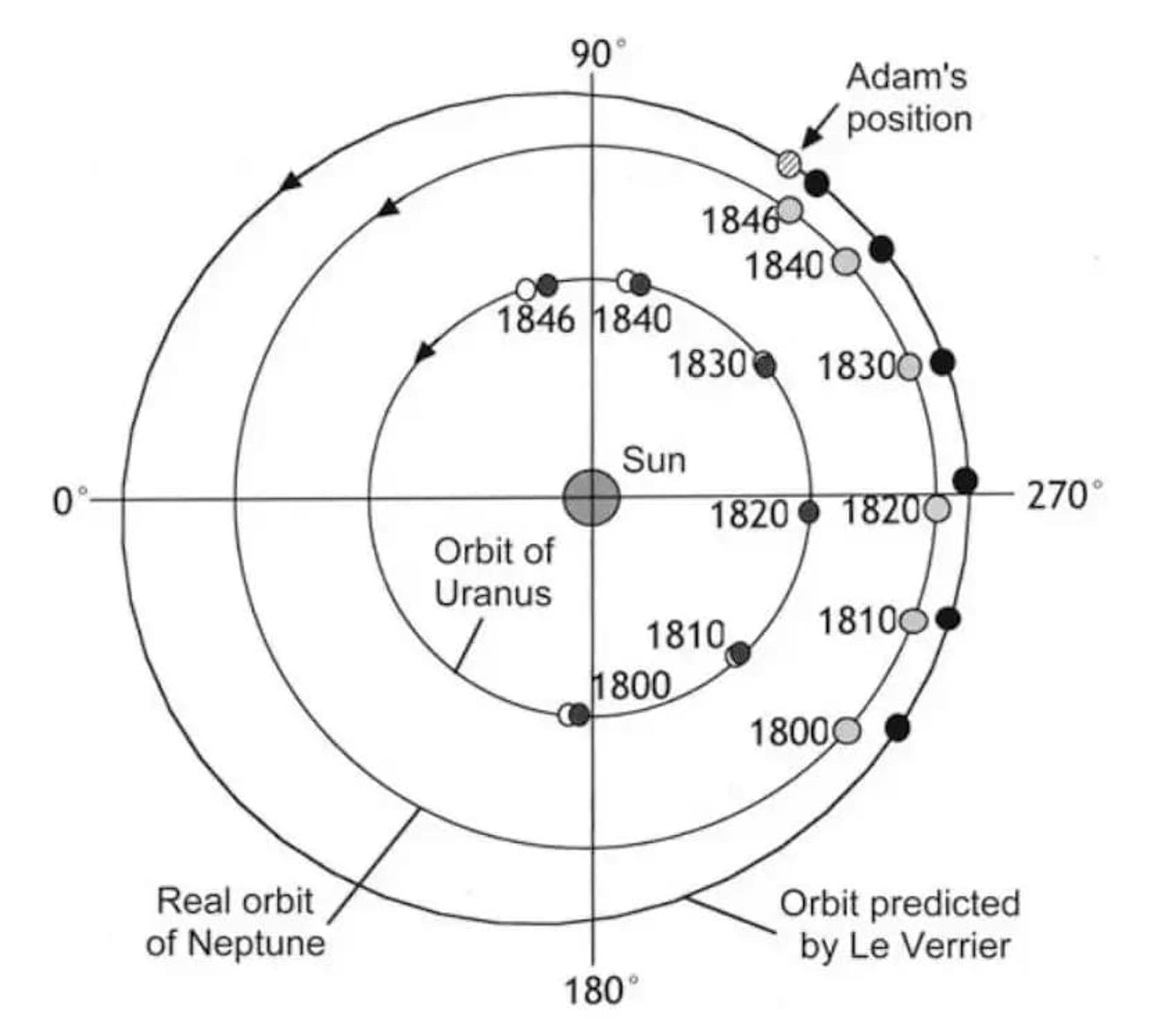
Từ năm 1845 đến 1846, nhà thiên văn học người Anh John Couch Adams, khi làm việc với vấn đề quỹ đạo của sao Thiên Vương, đã đề xuất ít nhất 5 và có thể là 6 vị trí tiềm năng cho một hành tinh giả định mới.

Tuy nhiên, việc phát hiện vẫn nằm ngoài tầm với do lỗi từ cả phía nhà lý thuyết và người quan sát. Trong khi đó, Urbain Le Verrier đã đưa ra dự đoán đầu tiên và duy nhất của ông vào năm 1846, dẫn đến việc khám phá gần như ngay lập tức khi lá thư của ông đến Đài quan sát Berlin.

Bước quan trọng nhất trong việc giải quyết vấn đề là thiết lập vấn đề một cách đúng đắn

Một trong những điều đầu tiên bạn học được, khi đối mặt với một vấn đề trong vật lý hoặc thiên văn học, là cách tiếp cận nó một cách có hệ thống. Bạn bắt đầu bằng cách xác định những gì đã biết và những gì cần phải biết, sau đó, dựa trên các mối quan hệ tồn tại giữa các đại lượng khác nhau đó, bạn cố gắng đề ra một kế hoạch từng bước để đạt được câu trả lời hoặc giải pháp cho những gì cần biết.

Trong khi hầu hết mọi người – đặc biệt là những người cảm thấy sợ hãi bởi vật lý hoặc toán học – lo lắng về việc thực hiện kế hoạch từng bước đó, bao gồm cả các bước đòi hỏi nhiều tính toán, thì sự thật là những bước đó chỉ là các kỹ năng. Nếu bạn mắc lỗi, điều đó không phải là thảm họa; sẽ có nhiều đồng nghiệp đủ năng lực giúp bạn phát hiện và sửa chữa nó.

Tuy nhiên, nếu bạn thiết lập vấn đề không đúng, toàn bộ cách tiếp cận của bạn sẽ sai. Dù bạn thực hiện các bước tiếp theo một cách hoàn hảo thế nào, bạn cũng chỉ đi đến giải pháp cho một vấn đề khác (và rất có thể không liên quan). Điều này có nghĩa là việc xác định:

– Những gì bạn biết,

– Những gì bạn cần biết,

– Các mối quan hệ chính giữa các đại lượng đó,

– Và cách tìm ra giải pháp (bao gồm cả việc đo lường hoặc thu thập dữ liệu để lấp đầy bất kỳ mảnh ghép quan trọng nào còn thiếu trên đường đi).

Là những khía cạnh quan trọng nhất để đi đến một giải pháp tiềm năng. Đúng là bạn (hoặc ai đó) cuối cùng cũng phải giải quyết vấn đề, nhưng việc tìm ra vấn đề thực sự cần giải quyết cũng như cách bạn sẽ giải quyết nó là các bước thiết yếu mà không cấp độ thành thạo toán học nào có thể thay thế.

Cảnh này mô tả các đường đánh dấu quỹ đạo của hành tinh và tàu vũ trụ, kèm theo nhãn về tốc độ, khoảng cách và ngày tháng. Sứ mệnh này có thể đưa chúng ta đến gần hơn với việc khám phá sự sống ngoài hành tinh trên mặt trăng băng giá Europa của sao Mộc.

Quỹ đạo bay của sứ mệnh Europa Clipper, bao gồm lần bay qua sao Hỏa vào đầu năm 2025, lần bay qua Trái Đất vào cuối năm 2026, và việc nó tiếp cận và cuối cùng bị hệ thống sao Mộc bắt giữ về mặt hấp dẫn vào đầu năm 2030. Bất chấp bức xạ của sao Mộc, quỹ đạo hình elip cực rộng của Europa Clipper sẽ cho phép thực hiện hàng chục lần tiếp cận gần với Europa trước khi tàu vũ trụ không còn hoạt động.

Một sự xấp xỉ đủ gần thường cũng tốt như một kết quả chính xác

Khi nhân loại khám phá Hệ Mặt Trời, một trong những công cụ quan trọng nhất của chúng ta là khả năng gửi tàu vũ trụ đến bất kỳ thế giới hoặc vật thể nào mà chúng ta quan tâm: để điều tra những gì chúng ta đang nghiên cứu ở cự ly gần hoặc tại chỗ. Chúng ta đã gửi tàu vũ trụ đến Mặt Trăng, sao Kim, và sao Hỏa từ những năm 1960. Kể từ đầu thế kỷ 21, chúng ta đã bay qua sao Diêm Vương, tiến gần hơn đến Mặt Trời hơn bao giờ hết, và có những sứ mệnh đang trên đường khám phá các mặt trăng băng giá của sao Mộc.

Lý thuyết về lực hấp dẫn tốt nhất của chúng ta đã tồn tại từ năm 1915: Thuyết tương đối rộng của Einstein, từ rất lâu trước khi bất kỳ vật thể nào do con người tạo ra phá vỡ lực hấp dẫn của Trái Đất.

Và rồi, khi chúng ta thực hiện các tính toán lý thuyết cần thiết để xác định các tàu vũ trụ cần ở vị trí nào và lúc nào để đạt được quỹ đạo đúng, chúng ta không sử dụng thuyết tương đối tổng quát.

Chúng ta chỉ sử dụng các phương trình của lực hấp dẫn Newton, mặc dù chúng ta biết rằng đó chỉ là một sự gần đúng thô sơ so với cách mô tả lực hấp dẫn chính xác và tổng quát hơn của Einstein. Lý do rất đơn giản và dễ hiểu:

– Việc giải quyết các vấn đề bằng các phương trình của Newton dễ hơn nhiều so với các phương trình của Einstein.

– Các phương trình của Newton đưa ra câu trả lời đủ chính xác với thực tế để các nhiệm vụ của chúng ta vẫn thành công, ngay cả khi không sử dụng các phương trình khó hơn của Einstein.

Biết khi nào cần dồn tài nguyên để giải một phiên bản khó hơn của một vấn đề, cũng như khi nào có thể tiết kiệm công sức, là một bài học quan trọng áp dụng được trong nhiều lĩnh vực, không chỉ riêng ngành vật lý thiên văn.

Ngôi sao biến quang RS Puppis, với các phản chiếu ánh sáng chiếu xuyên qua các đám mây giữa các vì sao. Các ngôi sao biến quang có rất nhiều dạng; một trong số đó là các sao biến quang Cepheid, có thể được đo lường cả trong dải Ngân Hà và các thiên hà cách xa từ 50 – 60 triệu năm ánh sáng, với tất cả các sao Cepheid đều thể hiện mối quan hệ giữa chu kỳ (thời gian cần để đạt độ sáng tối đa sau khi mờ đi) và độ sáng của chúng (độ sáng nội tại).

Hãy để mắt đến các mối quan hệ cơ bản giữa những thứ bạn có thể quan sát hoặc đo lường

Vào đầu thế kỷ 20, thiên văn học là một lĩnh vực gần như hoàn toàn do nam giới thống trị, và phụ nữ quan tâm đến lĩnh vực này thường bị giới hạn trong các vai trò xử lý dữ liệu, chẳng hạn như phân loại các ngôi sao dựa trên đặc tính của chúng.

Một trong những người phụ nữ đó là Henrietta Leavitt, người đã nhận thấy rằng một nhóm sao sáng nổi bật, có màu xanh (sao Cepheid), sẽ mờ đi và sáng lại theo chu kỳ. Cô phát hiện ra rằng:

– Ngôi sao càng sáng, chu kỳ biến đổi càng nhanh.

– Ngôi sao càng mờ, chu kỳ biến đổi càng chậm.

Mối quan hệ này được gọi là mối quan hệ chu kỳ–độ sáng, hoặc đôi khi được gọi bằng cái tên hiện đại hơn là Định Luật Leavitt.

Dù cho đến nay chúng ta vẫn chưa rõ tại sao mối quan hệ này tồn tại, nó đã đóng vai trò quan trọng trong việc xác định khoảng cách đến các thiên hà ngoài dải Ngân Hà. Edwin Hubble đã sử dụng mối quan hệ này để đo khoảng cách đến thiên hà Andromeda và các thiên hà gần đó, từ đó phát hiện ra vũ trụ đang giãn nở.

Ngày nay, các sao Cepheid được sử dụng như một chỉ báo khoảng cách đáng tin cậy: một công cụ vô giá trong việc xây dựng thang đo khoảng cách vũ trụ. Biết cách các đại lượng có thể đo lường được liên quan với nhau có thể là một mảnh ghép quan trọng trong việc giải quyết vấn đề, ngay cả khi bạn không hiểu hết bản chất của mối quan hệ đó.

Luôn nhận thức được rằng chuyên môn của bạn, dù sâu đến đâu, vẫn có giới hạn

Một trong những bài học khiêm tốn nhất đi kèm với bất kỳ nỗ lực khoa học nào là: sau nhiều năm, thậm chí nhiều thập kỷ nghiên cứu, ngay cả khi đã trở thành một chuyên gia hàng đầu thế giới trong lĩnh vực cụ thể của mình, bạn vẫn phải luôn nhận ra rằng sẽ có những người khác biết nhiều hơn bạn về các khía cạnh cụ thể của lĩnh vực đó.

Luôn có ai đó đã chuyên sâu hơn vào những gì bạn làm hoặc nghiên cứu, và bạn có thể học hỏi từ họ nếu sẵn lòng lắng nghe.

Mức độ khiêm nhường này không dễ đạt được; chúng ta thường trở thành nạn nhân của sự tự tin thái quá vào bản thân và những gì mình biết. Việc nhận ra giới hạn của chuyên môn và biết khi nào cần tìm thêm thông tin để hiểu rõ hơn và giải quyết vấn đề là một dấu ấn quan trọng trong sự phát triển của khoa học.

Từ Halley hỏi Newton về quỹ đạo của các sao chổi tuần hoàn, đến Einstein nhờ bạn mình Marcel Grossman giúp đỡ với toán học của không gian cong, lịch sử khoa học đã minh chứng cho giá trị của việc tìm kiếm sự giúp đỡ khi cần.

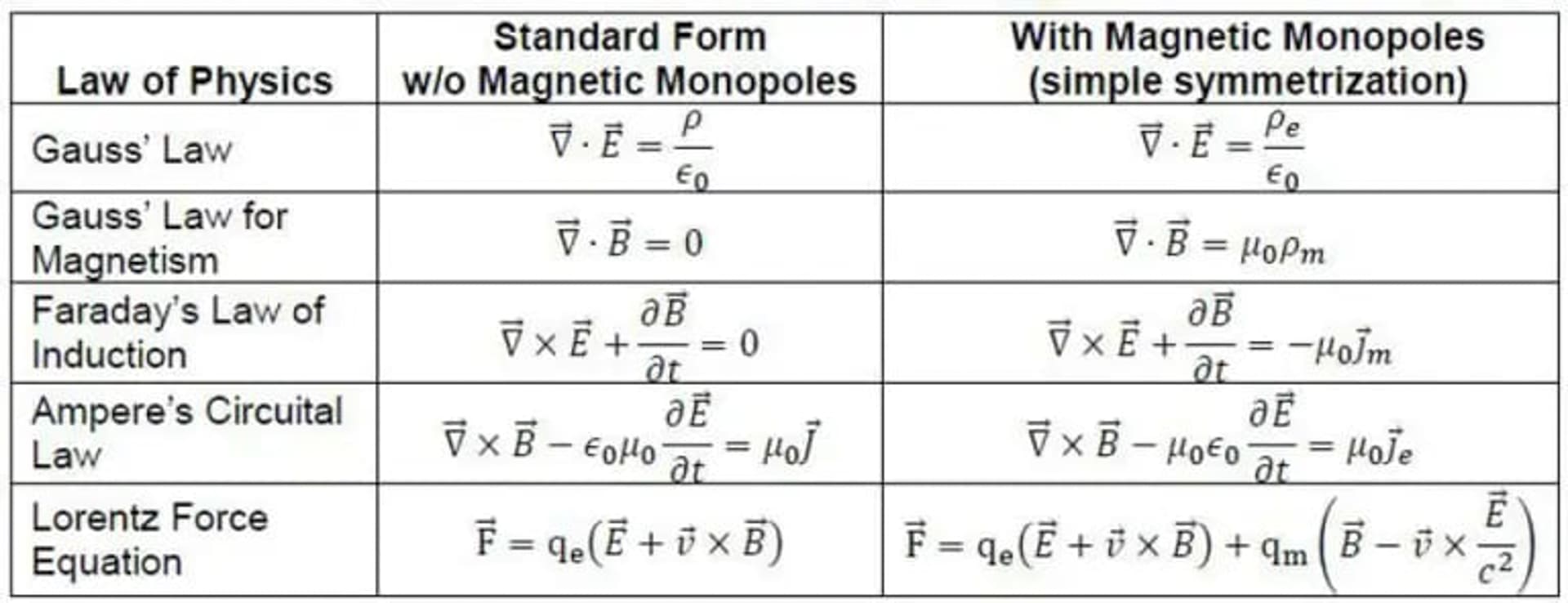
Nếu Einstein có thể nhận ra giới hạn trong chuyên môn của mình và tìm kiếm sự hỗ trợ khi cần thêm kỹ năng mà ông không có, thì có lẽ chúng ta cũng có thể đủ khiêm nhường để thừa nhận khi nào mình cần thêm thông tin để giải quyết các câu đố mà chúng ta đang đối mặt.

Biết được nơi tìm kiếm thông tin quan trọng hơn là ghi nhớ nó

Có một số thông tin chúng ta giữ trong đầu mọi lúc vì chúng được sử dụng thường xuyên và cần phải nhớ ngay lập tức. Tuy nhiên, những mẩu thông tin khác lại khó nhớ, ít được biết đến hoặc chỉ cần thiết trong những tình huống cụ thể.

Ví dụ, các nhà vật lý thiên văn có thể thường xuyên nhớ tốc độ ánh sáng trong chân không, nhưng hiếm khi cần nhớ chi tiết về tốc độ ánh sáng qua môi trường acrylic hay tốc độ âm thanh ở độ cao 16 km (10 dặm) so với mực nước biển.

Giải pháp cho vấn đề này không phải là ghi nhớ một lượng thông tin ngày càng lớn, mà là biết được nơi để tìm kiếm thông tin phù hợp bất cứ khi nào cần.

Trong khi sinh viên vật lý thường bị phê bình vì sử dụng sai công thức hoặc nhập giá trị không chính xác vào phương trình, thì giải pháp không phải là ghi nhớ tất cả mọi thứ cần thiết. Rất ít người có khả năng nhớ mọi thứ một cách hoàn hảo trong mọi tình huống.

Thay vào đó, việc biết được thông tin liên quan nằm ở đâu và có thể truy cập nó khi cần thiết là một bộ kỹ năng hữu ích hơn cho hầu hết mọi ứng dụng.

Hầu hết các vấn đề mà con người gặp phải không giống như một chương trình thi đấu kiến thức, nơi yêu cầu một câu trả lời tức thời và hoàn hảo cho một câu hỏi tương đối nhỏ.

Nhưng biết cách tìm và tiếp cận bất kỳ thông tin nào có thể liên quan đến các vấn đề mà bạn có khả năng gặp phải là một kỹ năng mà hầu hết mọi người nên rèn luyện.

Biết những khía cạnh nào của một vấn đề là không cần thiết có thể giúp bạn tránh bị phân tâm

Nếu bạn bắt đầu với một mẫu uranium – một trong những nguyên tố nặng nhất xuất hiện tự nhiên trong vũ trụ – nó sẽ không mãi mãi tồn tại dưới dạng uranium.

Đồng vị phổ biến nhất của uranium có 92 proton và 146 neutron, được gọi là uranium-238. Với chu kỳ bán rã là 4,5 tỷ năm, khoảng 50% uranium-238 được hình thành cùng thời điểm với Trái Đất (cách đây 4,5 tỷ năm) vẫn còn tồn tại trên hành tinh chúng ta ngày nay.

Tuy nhiên, uranium-238 không phân rã chỉ trong một bước đơn giản. Nó trải qua một chuỗi phân rã phức tạp, cuối cùng tạo thành chì-206 sau hàng triệu năm.

Khi giải quyết một vấn đề phức tạp, hiểu rõ điều gì là cần thiết và điều gì là không cần thiết có thể giúp bạn tránh bị sa đà vào các yếu tố không quan trọng. Đây là bài học quan trọng trong cả khoa học và cuộc sống: tập trung vào những gì thực sự ảnh hưởng đến mục tiêu cuối cùng của bạn.

Đây có thể dường như là một vấn đề cực kỳ khó khăn, vì uranium-238 không chỉ phân rã thành thorium-234 sau 4,5 tỷ năm. Thorium-234 cũng không ổn định và sẽ phân rã thành protactinium-234 với chu kỳ bán rã riêng của nó. Protactinium-234 cũng không ổn định, giống như sản phẩm phân rã của nó là uranium-234. Uranium-234 phân rã thành thorium-230, sau đó thorium-230 phân rã thành radon-226, và trên thực tế có tổng cộng 14 bước phân rã xảy ra trước khi đạt được kết quả cuối cùng ổn định là chì-206. Một số bước phân rã này chỉ kéo dài vài microgiây, trong khi những bước khác kéo dài vài phút, ngày, năm, hoặc thậm chí hàng thiên niên kỷ.

Và tuy nhiên, nếu bạn trả lời 50% còn lại là chì-206, bạn sẽ đúng hơn 99,9%; ít hơn 0,1% của uranium-238 ban đầu tồn tại dưới dạng của tất cả 13 bước khác trong chuỗi phân rã gộp lại. Thay vì thực hiện tính toán qua 14 bước, chỉ cần biết rằng, đối với vấn đề cụ thể này, chỉ có một bước là quan trọng và liên quan có thể giúp bạn tiết kiệm một lượng lớn thời gian và công sức. Điều này có ứng dụng rộng rãi đối với nhiều vấn đề mà chúng ta đối mặt, không chỉ trong lĩnh vực phân rã phóng xạ.

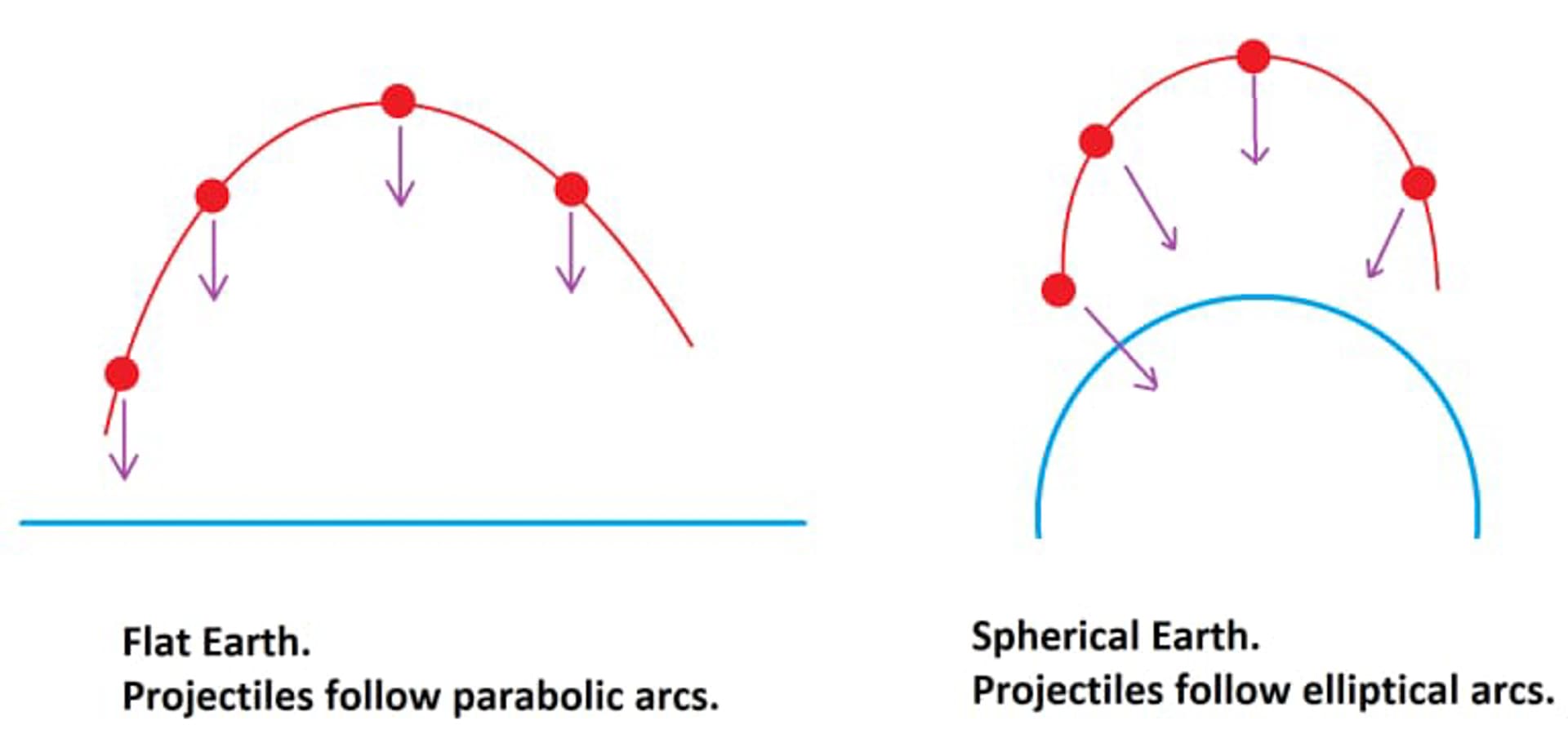
Nếu Trái Đất hoàn toàn phẳng và gia tốc ở mọi nơi đều hướng thẳng xuống, tất cả các vật thể bay sẽ tạo thành một đường parabol. Nhưng đối với các vật thể thực tế (mô tả phóng đại bên phải), gia tốc luôn hướng về tâm Trái Đất, nghĩa là quỹ đạo phải là một phần của đường cong elip, thay vì parabol.

Hầu như luôn có một lớp thực tại sâu hơn so với hiểu biết hiện tại của chúng ta

Khi hầu hết chúng ta bắt đầu học vật lý, chúng ta bắt đầu với cơ học: các vật thể rơi tự do và quả bóng lăn xuống dốc. Chúng ta giải các bài toán bằng đại số đơn giản, điều này hoàn toàn đủ cho những ứng dụng này. Sau đó, chúng ta học rằng vị trí, vận tốc và gia tốc không chỉ liên quan đến nhau mà còn là những khía cạnh của một phương trình vi phân: nơi một công thức mô tả cách chuyển động của một vật thay đổi từ khoảnh khắc này sang khoảnh khắc khác. Ở mức độ sâu hơn, bản chất lượng tử của thực tại dạy chúng ta rằng các đại lượng như vị trí không bao giờ có thể được đo chính xác hoàn toàn, mà luôn tồn tại một mức độ bất định vốn có.

Đây là mặt trái của bài học trước. Trong khi bỏ qua những phần thông tin không liên quan đến vấn đề có thể giúp bạn tiết kiệm thời gian và công sức, việc khám phá các mối quan hệ sâu sắc hơn giữa các khía cạnh khác nhau của bất kỳ hệ thống nào bạn đang nghiên cứu có thể dẫn đến khả năng dự đoán những hiện tượng mà nếu không thì sẽ rất bất ngờ và bí ẩn. Thông thường, thứ tự này bị đảo ngược, và chính sự xuất hiện của những hiện tượng bí ẩn và bất ngờ lại thúc đẩy chúng ta tìm kiếm một tập hợp các mối quan hệ sâu sắc hơn, trước đây chưa được phát hiện, giữa các đại lượng mà chúng ta quen thuộc. Chúng ta luôn phải nhớ rằng nhận thức của chúng ta về thực tại không phải là thực tại tự nó, mà chỉ là sự ước đoán tốt nhất của chúng ta về nó.

Có một năng lượng tích cực, không bằng không, vốn có trong các trường lượng tử: bao gồm trường bức xạ từ điện động lực học, trường sắc động lực học từ lực hạt nhân mạnh, và trường yếu từ lực hạt nhân yếu. Mặc dù những điều này thể hiện trong các tính toán của chúng ta dưới dạng các hạt ảo xuất hiện trong sơ đồ Feynman, chúng có các hiệu ứng vật lý thực sự, chẳng hạn như sự dịch Lamb và hiệu ứng Schwinger. Tổng năng lượng vốn có trong không gian không bao giờ có thể bằng không, nếu không sẽ dẫn đến các hậu quả không hợp lý.

Khi mọi thứ không thành công, hãy chuẩn bị để xem xét lại các giả định cơ bản của bạn

Điều này xảy ra thường xuyên hơn bạn nghĩ: chúng ta có một lý thuyết về cách một thứ gì đó nên hoạt động, chúng ta thực hiện các thí nghiệm quan trọng hoặc thực hiện các phép đo quan trọng, và những gì chúng ta tìm thấy lại khác với những gì chúng ta nghĩ. Câu hỏi lớn luôn là, Tại sao? Tại sao các dự đoán của chúng ta không khớp với những gì đã xảy ra? Có phải thí nghiệm hoặc phép đo của chúng ta có sai sót? Có phải chúng ta đã mắc sai lầm tính toán khi đưa ra dự đoán? Mặc dù đôi khi lỗi nằm ở những gì chúng ta đã làm, rất thường xuyên có một lỗi trong các giả định cơ bản mà chúng ta đã thực hiện khi thực hiện thí nghiệm hoặc dự đoán.

Có thể chúng ta đã bỏ qua một điều gì đó quan trọng đối với vấn đề đang được hỏi. Có thể chúng ta đã ngoại suy hành vi dự kiến của một hệ thống ra ngoài phạm vi hợp lệ đã được chứng minh. Có thể mô hình mà chúng ta đang sử dụng quá đơn giản và cần một mô hình phức tạp hơn. Hoặc, có thể các quy luật mà chúng ta kỳ vọng chi phối hệ thống cần được sửa đổi cho hệ thống cụ thể này, và theo đó là cho các hệ thống khác. Khía cạnh quan trọng nhất của khoa học là điều này: thế giới có thể được hiểu, nhưng sự hiểu biết của chúng ta về nó tại bất kỳ thời điểm nào chỉ mang tính tạm thời và luôn có thể sửa đổi. Nếu dữ liệu và dự đoán của chúng ta không khớp nhau, thường thì các giả định nằm dưới suy nghĩ của chúng ta là sai sót, và việc đặt câu hỏi với chúng là cách chúng ta tìm ra giải pháp cho các vấn đề dường như không thể giải quyết.

Phần này của khảo sát CEERS chứa nhiều loại thiên hà ở mọi khoảng cách, từ gần đến hơn 30 tỷ năm ánh sáng, được hình ảnh hóa bởi công cụ NIRCam của JWST. Một số thiên hà dường như đã phát triển quá lớn, quá nhanh đến mức các mô phỏng không thể giải thích được chúng. Tuy nhiên, một nghiên cứu mới phát hiện ra rằng một số thiên hà sơ khai đó thực ra ít lớn hơn nhiều so với hình dáng ban đầu của chúng, và độ sáng của chúng được tăng cường bởi cả sự hình thành sao bùng nổ và ánh sáng phát ra từ các hố đen siêu khối lượng hoạt động bên trong chúng.

Có một lời khuyên tôi nhận được từ một giáo sư toán khi tôi học năm đầu đại học. Vào đầu một khóa học về phương trình vi phân, ông cảnh báo chúng tôi rằng: Hầu hết các phương trình vi phân đều không thể giải. Và hầu hết các phương trình vi phân có thể giải thì bạn cũng không thể giải được. Điều này nhấn mạnh hai khía cạnh quan trọng trong việc học.

Không phải mọi vấn đề bạn gặp phải đều là vấn đề bạn có thể giải quyết chính xác, mà đúng hơn chỉ là điều bạn có thể cố gắng hết sức để đạt được đáp án phù hợp nhất cho nhu cầu cụ thể của bạn.

Tuy nhiên, nếu bạn cần một giải pháp, bạn nên chuẩn bị không chỉ để cố gắng hết sức mà còn tận dụng tất cả những công trình đã có trước đó về chủ đề này; câu trả lời mà bạn đang tìm kiếm có thể vượt quá khả năng của bạn, nhưng không vượt quá khả năng của những người đã từng đối mặt với nó.

Khi hầu hết chúng ta nghĩ về việc học, chúng ta nghĩ về kiến thức mà chúng ta có được thông qua kinh nghiệm, nghiên cứu hoặc thực hành. Nhưng bản thân việc học còn hơn thế: nó là một nghệ thuật, một kỹ năng, và chỉ có thể diễn ra nếu bạn có khả năng nhận ra khi nào những gì bạn biết chưa đủ để kể câu chuyện đầy đủ và toàn diện về vấn đề bạn đang đối mặt. Tám bài học này, ngay cả khi bạn không phải là một nhà vật lý thiên văn, vẫn có thể giúp mọi người trở thành một người học tốt hơn.