Tầm quan trọng của việc phân biệt trọng lượng và khối lượng
Ở Trái Đất, chúng ta thường sử dụng các thuật ngữ như trọng lượng (đo bằng pound) và khối lượng (đo bằng kilogram) như thể chúng có thể thay thế cho nhau. Nhưng chúng thực sự không giống nhau.
· 22 phút đọc lượt xem.
Ở Trái Đất, chúng ta thường sử dụng các thuật ngữ như trọng lượng (đo bằng pound) và khối lượng (đo bằng kilogram) như thể chúng có thể thay thế cho nhau. Nhưng chúng thực sự không giống nhau.
Trọng lượng và khối lượng không phải là một
Ở Trái Đất, chúng ta thường sử dụng các thuật ngữ như trọng lượng (đo bằng pound) và khối lượng (đo bằng kilogram) như thể chúng có thể thay thế cho nhau. Nhưng trọng lượng và khối lượng thực sự không giống nhau.
Nếu bạn hỏi ai đó họ nặng bao nhiêu, họ có thể đưa ra một con số từ chiếc cân mà họ đọc được. Nếu người đó sử dụng hệ đo lường mét, họ có thể nói rằng khối lượng của họ là 93 kilogram, chẳng hạn. Nếu họ sử dụng hệ đo lường Anh, con số tương ứng sẽ là 205 pound. Thông thường, trên bề mặt Trái Đất, chúng ta có thể chuyển đổi giữa hai đơn vị này bằng một phép tính đơn giản: 1 kilogram tương đương với 2.205 pound, và ngược lại, 2.205 pound chuyển đổi thành 1 kilogram. Việc chuyển đổi qua lại chỉ cần nhân hoặc chia, điều này có vẻ khá dễ dàng.
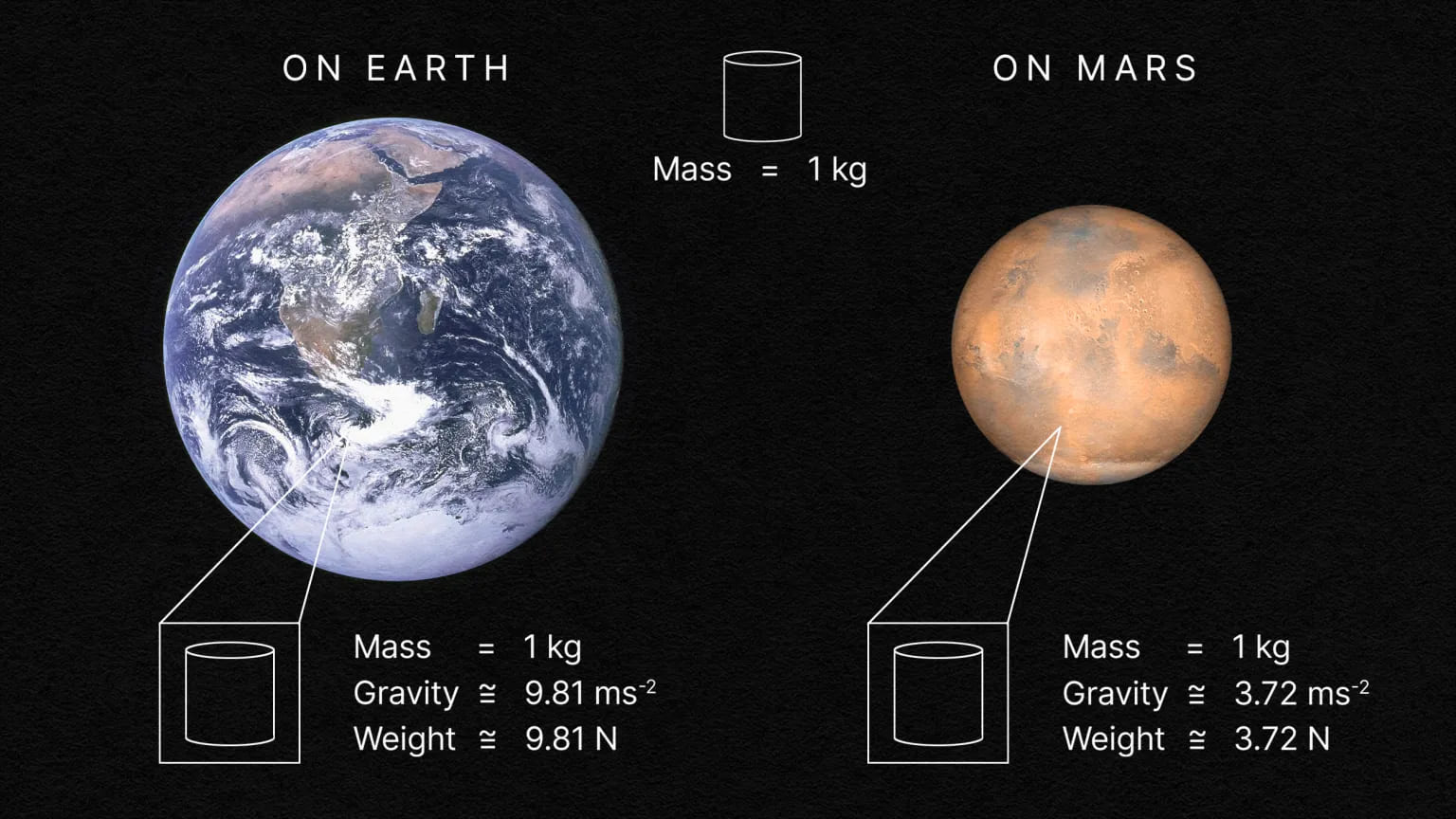
Nhưng kilogram và pound không chỉ là đơn vị đo trọng lượng trong các hệ thống đo lường khác nhau; chúng là những khái niệm hoàn toàn khác nhau. Kilogram là một đơn vị đo khối lượng, không phải trọng lượng, trong khi pound là một đơn vị đo trọng lượng, không phải khối lượng. Chỉ trên bề mặt Trái Đất, nơi chúng ta đứng yên so với Trái Đất đang quay, hai khái niệm này mới có thể được sử dụng thay thế cho nhau một cách hợp lý.
Không phải đến khi Isaac Newton xuất hiện, sự khác biệt giữa trọng lượng và khối lượng mới được đánh giá đúng mức. Ngay cả các giáo viên vật lý (và sách giáo khoa vật lý) đôi khi cũng nhầm lẫn về việc hai khái niệm này không giống nhau. Đây là lý do tại sao sự thật tưởng chừng đơn giản này – rằng trọng lượng và khối lượng khác nhau – lại rất sâu sắc.

Theo truyền thuyết, thí nghiệm đầu tiên chứng minh rằng mọi vật rơi với cùng tốc độ, bất kể khối lượng, được Galileo Galilei thực hiện trên tháp nghiêng Pisa. Bất kỳ hai vật nào được thả trong trường trọng lực, nếu không tính đến hoặc bỏ qua lực cản của không khí, sẽ rơi xuống đất với cùng tốc độ và sẽ di chuyển quãng đường tỷ lệ thuận với bình phương thời gian rơi tự do.
Quả cầu không tách khỏi tháp, điều mà một số người (sai lầm) cho rằng sẽ xảy ra nếu Trái Đất quay.
Những thí nghiệm đầu tiên giúp chúng ta hiểu về trọng lực và chuyển động được thực hiện ngay tại Trái Đất: bằng cách thả các vật trong trạng thái rơi tự do hoặc cho chúng lăn xuống các dốc nghiêng.
Nếu bạn thả một vật từ trạng thái đứng yên, nó sẽ rơi thẳng xuống, tăng tốc với một tốc độ không đổi. Tốc độ của nó sẽ tăng tỷ lệ thuận với thời gian rơi, và quãng đường mà nó đi được sẽ tỷ lệ thuận với bình phương thời gian rơi.
Đối với các vật lăn xuống dốc, sự tỷ lệ vẫn giống hệt, nhưng gia tốc tổng thể – và do đó, sự tăng tốc và thay đổi quãng đường – thấp hơn so với các vật trong trạng thái rơi tự do.
Hiện tượng này, tuy nhiên, dường như không phụ thuộc vào khối lượng hay trọng lượng. Một vật nhẹ sẽ rơi nhanh như một vật nặng, đặc biệt nếu lực cản của không khí không phải là yếu tố. Một viên đá chì nhỏ và một quả cầu chì lớn sẽ rơi và tăng tốc với cùng tốc độ, và chúng cũng sẽ lăn xuống dốc trong cùng khoảng thời gian.
Tuy nhiên, quả cầu lớn hơn có khối lượng và trọng lượng lớn hơn viên đá nhỏ. Bạn có thể kiểm chứng điều này bằng cách sử dụng một chiếc cân: một thiết bị hoặc đặt các khối lượng lên một đầu cân để đối trọng với khối lượng của bạn, hoặc một thiết bị đo trực tiếp lực được tạo ra thông qua bàn chân của bạn (hoặc bất kỳ bộ phận nào tiếp xúc với thiết bị) lên chính chiếc cân đó.

Cán cân công lý tượng trưng cho việc trọng lượng của các lập luận mạnh mẽ nhất sẽ nghiêng về phía công lý hơn. Không giống như chiếc cân thông thường, loại cân hai bên này cho phép bạn xác định chính xác khối lượng của một vật trong mọi điều kiện môi trường, ngoại trừ trạng thái không trọng lượng hoàn hảo.
Hai loại cân này, thật thú vị, thực hiện các phép đo hoàn toàn khác nhau. Có một cách đơn giản để kiểm chứng điều này: bằng một thang máy. Nếu bạn cân bằng hai bên của một chiếc cân – như chiếc cân cán cân công lý nổi tiếng, đặt hai bộ khối lượng ở hai bên một điểm cân bằng – thì chiếc cân đó sẽ vẫn cân bằng. Điều này đúng trong mọi tình huống thang máy:
– Đứng yên trên bề mặt Trái Đất,
– Tăng tốc đi lên,
– Tăng tốc đi xuống,
– Hoặc đứng yên trên bất kỳ hành tinh nào khác.
Cùng một khối lượng sẽ cân bằng chiếc cân trên Trái Đất và dưới mọi gia tốc mà bạn có thể tưởng tượng. Điều này là do lực hấp dẫn hướng xuống, tác động lên khối lượng ở một bên cân, cân bằng với lực hấp dẫn hướng xuống tác động lên khối lượng (tương đương) ở bên kia cân.
Nhưng nếu bạn sử dụng một chiếc cân hoạt động bằng cách đo lực đẩy lên thông qua bàn chân bạn (và giữ bạn không rơi qua cân), bạn sẽ thấy rằng những tình huống tương tự trong thang máy:
– Đứng yên trên bề mặt Trái Đất,
– Tăng tốc đi lên,
– Tăng tốc đi xuống,
– Hoặc đứng yên trên bất kỳ hành tinh nào khác,

Sẽ đưa ra các kết quả khác nhau trong từng trường hợp. Chỉ khi bạn đứng yên trên bề mặt Trái Đất, chiếc cân mới đưa ra kết quả giống với loại cân kia. Cân nặng này, hơn 100 năm trước, đã cân bằng lực hấp dẫn từ các vật phía trên cân với một lò xo nội bộ.
Tại sao cân nặng của bạn thay đổi trong các tình huống khác nhau?
Lượng nén của lò xo phụ thuộc vào lực hấp dẫn từ các vật phía trên nó. Nếu khối lượng hoặc gia tốc của các vật thay đổi, kết quả đọc của cân cũng sẽ thay đổi.
Trong bộ ví dụ thứ hai, bạn đang đo cân nặng trực tiếp qua lực mà cân phải dùng để đẩy bạn lên. Cân nặng thực chất là một ví dụ của lực, tuân theo định luật nổi tiếng của Newton: F = ma. Nếu bạn đứng yên, trọng lực sẽ cố gắng gia tốc bạn xuống dưới với một lực cụ thể, nơi gia tốc đó là do trọng lực của Trái Đất ở bề mặt. Gia tốc này được gọi là g, có giá trị khoảng 9,8 mét trên giây bình phương, hướng về tâm Trái Đất.
Cân sẽ phải đẩy lại với một lực bằng và ngược chiều để giữ bạn không rơi qua cân. Điều này dẫn đến định nghĩa tiêu chuẩn về cân nặng trên bề mặt Trái Đất: khối lượng của bạn nhân với g, hoặc 9,8 m/s².

Nếu bạn đứng trên cân khi thang máy gia tốc đi lên, chẳng hạn ngay sau khi bấm nút lên tầng trên cùng, bạn không chỉ chịu gia tốc của trọng lực Trái Đất mà còn cả gia tốc đi lên của thang máy. Trong trường hợp này, cân không chỉ phản ứng với trọng lực của bạn mà còn phải tạo thêm lực để gia tốc bạn đi lên. Lúc này, cân đọc ma, trong đó a bằng g cộng thêm gia tốc đi lên.
Ngược lại, nếu thang máy gia tốc đi xuống, cân sẽ đọc ít hơn trọng lượng khi đứng yên trên mặt đất. Vì gia tốc lúc này là g trừ đi gia tốc đi xuống thêm vào.
Loại cân này đo lực mà chân bạn tác động lên nó, và kết quả có thể thay đổi tùy thuộc vào điều kiện gia tốc. Ngược lại, cân đối trọng cho một kết quả nhất quán vì nó dựa vào việc cân bằng khối lượng. Khối lượng ở phía đối diện của cân luôn chịu cùng gia tốc như bạn, bất kể bạn ở trên Trái Đất, trong thang máy, hay trên một hành tinh khác.
Khối lượng là đặc tính vốn có của các nguyên tử cấu thành cơ thể bạn, trong khi cân nặng phụ thuộc vào gia tốc của các nguyên tử đó dưới ảnh hưởng của các lực.
Khối lượng và trọng lực: Góc nhìn từ Newton
Newton đã sử dụng những gì xảy ra trên bề mặt Trái Đất để so sánh với những hiện tượng xa xôi, như Mặt Trăng. Ông nhận ra rằng trọng lực cũng là lực thống trị hành vi của Mặt Trăng, tương tự như cách nó ảnh hưởng đến các vật thể trên Trái Đất.
Nhà khoa học Hy Lạp cổ đại Aristarchus đã sử dụng bóng của Trái Đất trong các lần nguyệt thực để tính toán khoảng cách tới Mặt Trăng từ hơn 2000 năm trước. Phương pháp này vẫn được sử dụng ngày nay, với độ chính xác cải thiện nhờ thí nghiệm đo khoảng cách bằng laser từ Mặt Trăng.
Như Aristarchus đã lập luận, trong một lần nguyệt thực, các tia sáng từ Mặt Trời chiếu tới Trái Đất sẽ tạo ra một cái bóng. Khi Mặt Trăng đi qua bóng đó, phần bóng của Trái Đất rơi lên Mặt Trăng sẽ chứa đựng thông tin hữu ích về kích thước tương đối giữa Trái Đất và Mặt Trăng. Dựa trên đó, chúng ta có thể xác định được khoảng cách tới Mặt Trăng.

Phương pháp này đã được sử dụng suốt hàng thiên niên kỷ, và cho tới nay, nó vẫn còn giá trị. Tuy nhiên, các thí nghiệm đo khoảng cách bằng tia laser hiện đại cho phép chúng ta xác định khoảng cách từ Trái Đất đến Mặt Trăng với độ chính xác cao hơn rất nhiều.
Sự khác biệt giữa khối lượng và cân nặng vẫn là một trong những bài học quan trọng trong vật lý. Có rất nhiều sách giáo khoa (và cả giáo viên vật lý) thường đơn giản hóa vấn đề và tuyên bố rằng cân nặng W luôn tuân theo phương trình W = mg. Điều này là không chính xác, vì phương trình này chỉ đúng khi bạn đứng yên trên bề mặt Trái Đất.
Thậm chí, ngay cả khi đứng yên, g – gia tốc do trọng lực của Trái Đất – cũng không hoàn toàn cố định. Giá trị của g thay đổi từ khoảng 9,78 m/s² tại các cao nguyên gần xích đạo lên tới 9,83 m/s² tại mực nước biển ở các vùng cực của Trái Đất. Điều này là do Trái Đất không phải là một hình cầu hoàn hảo; nó phình ra ở xích đạo và dẹt lại ở các cực.
Tuy nhiên, không phải việc quan sát cân nặng và khối lượng trên Trái Đất đã giúp Newton hiểu về trọng lực. Thay vào đó, ông đã so sánh những gì xảy ra trên bề mặt Trái Đất với các hiện tượng xảy ra ở xa Trái Đất, cụ thể là trên Mặt Trăng.
Trong các lần nguyệt thực, bóng của Trái Đất được chiếu lên Mặt Trăng và che khuất ánh sáng từ Mặt Trời. Việc tái tạo kích thước bóng của Trái Đất so với kích thước thực tế của Mặt Trăng là một trong những phương pháp lâu đời nhất để đo khoảng cách tới Mặt Trăng. Đây là một phương pháp đã được Aristarchus khai thác từ thế kỷ thứ 3 TCN.
Ngày nay, nhờ sự tiến bộ của khoa học, chúng ta có thể tái tạo các hiện tượng nguyệt thực thông qua hình ảnh mô phỏng và xác định kích thước bóng cũng như khoảng cách tới Mặt Trăng một cách chính xác hơn bao giờ hết. Những thí nghiệm hiện đại như đo khoảng cách laser tới Mặt Trăng đã hoàn thiện thêm sự hiểu biết của chúng ta về mối quan hệ giữa Trái Đất và vệ tinh của nó.
Điều Newton nhận ra là hai sự thật đơn giản. Đầu tiên, so với kích thước của Trái Đất – bán kính của nó chỉ xấp xỉ dưới 6400 km – thì Mặt Trăng cách Trái Đất khoảng 60 lần khoảng cách này, tức khoảng 380.000 km. Thứ hai, thời gian để Mặt Trăng hoàn thành một vòng quay 360° quanh Trái Đất vào khoảng 27,3 ngày, tương ứng với độ dài của một tháng thiên văn khi trừ đi chuyển động của Trái Đất quanh Mặt Trời, còn được gọi là tháng sao.
Khi xem xét khoảng cách mà Mặt Trăng di chuyển để hoàn thành một vòng quay quanh Trái Đất trong khoảng thời gian của một tháng sao, Newton ngay lập tức nhận ra rằng gia tốc trọng trường của Mặt Trăng không thể tương đương với gia tốc trọng trường của các vật thể trên bề mặt Trái Đất. Nó phải nhỏ hơn rất nhiều.

Trái Đất, Mặt Trăng và khoảng cách giữa chúng theo tỷ lệ. Lực hấp dẫn giữa Trái Đất và Mặt Trăng tỷ lệ nghịch với bình phương khoảng cách giữa chúng, nghĩa là nếu Mặt Trăng chỉ cách một nửa khoảng cách hiện tại, thì lực hấp dẫn và gia tốc của Mặt Trăng sẽ tăng gấp bốn lần. Ngược lại, nếu khoảng cách tăng gấp đôi, lực hấp dẫn (và do đó, gia tốc của Mặt Trăng) sẽ giảm đi một phần tư. Mặt Trăng hiện cách tâm Trái Đất khoảng 60 lần khoảng cách từ bề mặt Trái Đất đến tâm Trái Đất.
Thực tế, gia tốc của Mặt Trăng do lực hấp dẫn phải nhỏ hơn hàng ngàn lần so với gia tốc trên bề mặt Trái Đất. Nó chỉ khoảng 0,0026 m/s² để duy trì tốc độ và vị trí của Mặt Trăng so với hành tinh của chúng ta, thay vì 9,8 m/s² như trên bề mặt Trái Đất.
Con số ~3700 này đến từ đâu? Nó bắt nguồn từ sự thật mà Newton nhanh chóng suy luận được: gia tốc trọng trường mà một vật thể chịu từ vật thể khác tỷ lệ nghịch với bình phương khoảng cách giữa chúng. Vì Mặt Trăng cách tâm Trái Đất 61 lần so với bề mặt Trái Đất, nên gia tốc trọng trường của Mặt Trăng do Trái Đất gây ra chỉ bằng 1/61² (hoặc 1/3721) so với một vật thể chịu gia tốc trên bề mặt Trái Đất.
Nói cách khác, nếu bạn không đứng trên bề mặt Trái Đất mà thay vào đó đứng ở khoảng cách của Mặt Trăng với Trái Đất, nhưng vẫn trên một nền tảng được neo vào Trái Đất, bạn sẽ đo được cân nặng của mình chỉ bằng 0,027% so với cân nặng thông thường mà bạn đo được trên bề mặt Trái Đất. Cân nặng của bạn không chỉ phụ thuộc vào khối lượng mà còn phụ thuộc vào gia tốc.
Nhiệm Vụ Apollo 10 và trọng lực
Apollo 10, được gọi là buổi diễn tập cho việc đổ bộ Mặt Trăng, được trang bị đầy đủ các thiết bị cho phép họ hạ cánh trên bề mặt Mặt Trăng. Họ đã tiến gần Mặt Trăng hơn bất kỳ sứ mệnh có người lái nào trước đó và mở đường cho cuộc đổ bộ thực sự diễn ra với Apollo 11 vào tháng 7 năm 1969. Toàn bộ nhiệm vụ chỉ yêu cầu vật lý Newton, và các phi hành gia trên quỹ đạo quanh Mặt Trăng cảm thấy mình hoàn toàn không trọng lượng.

Tuy nhiên, các phi hành gia rời xa Trái Đất – dù trong quỹ đạo thấp quanh Trái Đất, quỹ đạo quanh Mặt Trăng hay thậm chí trên bề mặt Mặt Trăng – không bao giờ trải nghiệm giảm cân như bạn mong đợi khi áp dụng các phương trình của Newton. Thay vào đó, các hiện tượng sau xảy ra:
-
Một phi hành gia trong quỹ đạo thấp quanh Trái Đất, chẳng hạn như trên Trạm Vũ trụ Quốc tế, cảm thấy mình không trọng lượng. Khối lượng của họ không thay đổi, và khoảng cách từ tâm Trái Đất chỉ tăng vài trăm km so với trên bề mặt, nhưng họ cảm nhận cân nặng của mình bằng 0. Trên cân, họ không đo được dù chỉ một gram lực.
-
Một phi hành gia trong quỹ đạo quanh Mặt Trăng, như phi hành đoàn của Apollo 8 khi lần đầu tiên trở thành những người đầu tiên bay quanh Mặt Trăng, cũng cảm thấy mình không trọng lượng. Một lần nữa, dù khối lượng của họ không thay đổi và khoảng cách của họ từ Trái Đất lớn hơn so với các phi hành gia trong quỹ đạo thấp, họ vẫn không đo được cân nặng của mình.
-
Một phi hành gia trên bề mặt Mặt Trăng sẽ không ở trạng thái không trọng lượng; cân nặng của họ sẽ bằng mg, nhưng lần này, g là gia tốc trọng trường trên bề mặt Mặt Trăng, không phải của Trái Đất, tương ứng với cân nặng của họ chỉ bằng khoảng 16% so với trên bề mặt Trái Đất.
Cân nặng của bạn không phải là một đại lượng khách quan; nó thậm chí không chỉ đơn thuần là khối lượng nhân với gia tốc. Thay vào đó, cân nặng là cảm giác bạn trải nghiệm khi có một lực gia tốc bạn so với môi trường của mình, chẳng hạn như lực của mặt đất (hoặc ghế ngồi) giữ bạn không rơi qua Trái Đất dưới ảnh hưởng của trọng lực.

Nguyên tắc tương đương khẳng định rằng không có sự khác biệt giữa gia tốc do trọng lực và gia tốc do bất kỳ lực nào khác trong vũ trụ. Vì một lực phụ thuộc vào hằng số hấp dẫn và lực còn lại thì không, việc kiểm tra nguyên tắc tương đương là một cách để giới hạn sự thay đổi theo thời gian của hằng số hấp dẫn. Đến nay, thử nghiệm chính xác nhất của nguyên tắc này được thực hiện bởi vệ tinh MICROSCOPE, chứng minh sự tương đương giữa khối lượng hấp dẫn và khối lượng quán tính với sai số chỉ 1 phần trong 10^15.
Chúng ta thường nói về việc kiểm soát cân nặng hay giảm cân, nhưng nếu đó thực sự là mục tiêu của bạn, bạn chỉ cần đi lên độ cao lớn hơn, di chuyển đến hành tinh khác hoặc bước vào thang máy và chờ cánh cửa đóng lại sau khi nhấn nút xuống. Tuy nhiên, không điều nào trong số này mang lại kết quả bạn mong muốn, vì bạn không thực sự muốn thay đổi, kiểm soát hay quản lý cân nặng của mình; điều bạn quan tâm là khối lượng – một thuộc tính vật lý vốn có của bạn. Cân nặng chỉ là một hệ quả phụ của việc bạn có khối lượng nhất định trong khi đồng thời nằm trên bề mặt Trái Đất và ở trạng thái nghỉ so với bề mặt đó.
Nếu bạn đang đọc bài viết này trong một căn phòng kín, có thể bạn sẽ ngạc nhiên khi biết rằng cân nặng của bạn – chính cảm giác bạn đang cảm nhận trong cơ thể ngay bây giờ – là không đủ để nói rằng bạn đang đứng yên trên Trái Đất. Bạn hoàn toàn có thể đang ở trong một tàu vũ trụ hoặc tên lửa đang gia tốc lên trên, và bạn sẽ cảm nhận cân nặng của mình giống hệt như bạn cảm nhận ở đây và ngay lúc này. Không có sự khác biệt cơ bản nào giữa trọng lực và bất kỳ gia tốc nào khác, mặc dù điều này chỉ được tiết lộ khi Einstein lần đầu đưa ra lý thuyết của mình. Tuy nhiên, để học về cân nặng, và cụ thể là sự khác biệt giữa cân nặng và khối lượng, chúng ta chỉ cần cái nhìn sâu sắc từ Newton. Như Matt Strassler đã viết trong cuốn sách mới hấp dẫn của ông:
Tư duy của chúng ta ngày nay không vượt trội hơn so với vài thế kỷ hay thậm chí vài thiên niên kỷ trước. Những gì từng khó hiểu về mặt khái niệm với trí óc con người khi đó vẫn còn khó hiểu bây giờ. Sự khác biệt quan trọng nhất giữa tổ tiên chúng ta và chúng ta chỉ đơn giản là thế này: họ sống trước Newton, còn chúng ta sống sau Newton.







