Liệu lạm phát vũ trụ có vi phạm định luật bảo toàn năng lượng không?

Một số đại lượng vật lý, trong tất cả các thí nghiệm thực hiện trong phòng thí nghiệm, luôn được bảo toàn: bao gồm năng lượng. Nhưng đối với toàn bộ vũ trụ? Không hẳn vậy.

Mở đầu

Trong vũ trụ luôn thay đổi của chúng ta, có một vài thứ mà chúng ta có thể tin tưởng rằng sẽ giữ nguyên không đổi và bất biến. Từ nơi này đến nơi khác và từ khoảnh khắc này sang khoảnh khắc khác, các định luật vật lý không thay đổi, chúng vẫn giữ nguyên và được áp dụng đồng đều trên toàn bộ vũ trụ. Các giá trị của các hằng số cơ bản – những tham số quyết định khối lượng của các hạt và cường độ của các lực – không thay đổi theo thời gian hay không gian. Và trong mọi thí nghiệm mà chúng ta từng thực hiện, chúng ta thấy rằng một số đại lượng luôn được bảo toàn: tổng lượng bạn bắt đầu sẽ luôn bằng tổng lượng bạn kết thúc.

Có rất nhiều đại lượng được bảo toàn: điện tích, động lượng tuyến tính, động lượng góc, và tất nhiên, năng lượng. Định luật bảo toàn năng lượng có lẽ là định luật bảo toàn nổi tiếng nhất, và nó áp dụng cho các vật thể trên Trái Đất cũng như cho Hệ Mặt Trời, các ngôi sao, và toàn bộ Dải Ngân Hà. Nhưng nếu bạn quay ngược thời gian trở lại lịch sử vũ trụ, liệu bạn có thể phát hiện ra rằng, chỉ có thể, năng lượng không được bảo toàn sau tất cả? Đó là điều mà Michael Genovese muốn biết, khi hỏi:

Nếu mật độ trường năng lượng vẫn giữ nguyên trong suốt lạm phát vũ trụ, điều đó có phù hợp với nguyên lý bảo toàn năng lượng không (vì năng lượng sẽ tăng lên theo cấp số nhân khi không gian tăng và mật độ vẫn ổn định)?

Câu trả lời, dù có thể gây sốc khi nghe, là năng lượng không phải lúc nào cũng được bảo toàn, và lạm phát vũ trụ thực sự vi phạm bảo toàn năng lượng theo một cách đặc biệt cực đoan. Đây là những gì đang xảy ra.

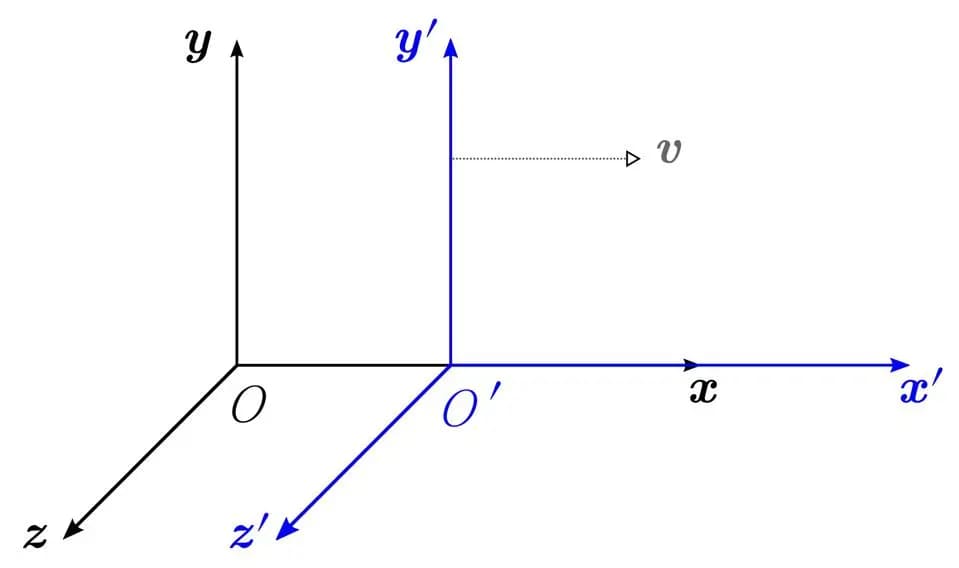
Các khung tham chiếu khác nhau, bao gồm các vị trí và chuyển động khác nhau, sẽ thấy các định luật vật lý khác nhau (và sẽ không đồng ý về thực tại) nếu một lý thuyết không bất biến theo thuyết tương đối. Việc chúng ta có một đối xứng dưới dạng gia tốc, hay các biến đổi vận tốc, cho chúng ta biết rằng chúng ta có một đại lượng được bảo toàn: động lượng tuyến tính. Việc một lý thuyết bất biến dưới bất kỳ loại biến đổi tọa độ hay vận tốc nào được gọi là bất biến Lorentz, và bất kỳ đối xứng bất biến Lorentz nào cũng bảo toàn đối xứng CPT. Khái niệm về bất biến dưới chuyển động không đổi này có từ thời Galileo.

Hóa ra, nếu bạn muốn biết cái gì được bảo toàn trong vũ trụ, bạn cần một thứ cụ thể làm nền tảng cho các quy tắc chi phối hệ thống của bạn: một đối xứng. Có những mối liên hệ sâu sắc giữa các đối xứng và các đại lượng được bảo toàn, và chúng được tiết lộ lần đầu tiên hơn một trăm năm trước bởi một trong những anh hùng không được ca ngợi của vật lý và toán học: Emmy Noether. Bà đã viết hai chứng minh quan trọng, được công bố vào năm 1915, trong đó nội dung cho thấy lần đầu tiên rằng nếu bạn có ba tiêu chí sau:

– Một hệ thống vật lý,

– nơi các lực tác động là bảo toàn (lực của một vật thể tác động lên vật thể khác dẫn đến một lực bằng và ngược lại tác động lên vật thể đầu tiên),

– mà hành động của nó có một đối xứng khả vi,

Thì mỗi và mọi đối xứng khả vi độc lập mà nó sở hữu cũng sẽ dẫn đến một định luật bảo toàn liên quan. Nếu có một định luật bảo toàn, thì có một đại lượng được bảo toàn. Đó là cốt lõi của mối liên hệ sâu sắc giữa các đại lượng được bảo toàn (như năng lượng) và các định luật bảo toàn và đối xứng nói chung.

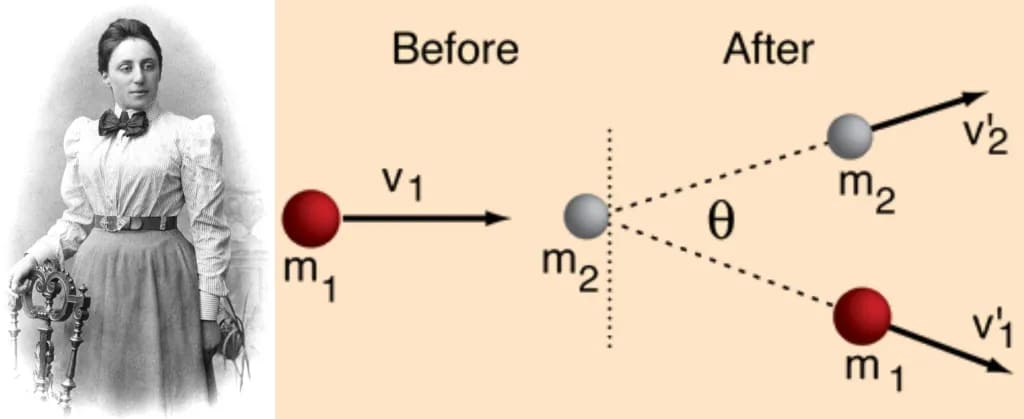
Emmy Noether, người đã chứng minh định lý Noether, liên kết các đối xứng và bất biến của một lý thuyết với một đại lượng được bảo toàn liên quan. Ở bên phải, hình minh họa về bảo toàn động lượng tuyến tính, một hệ quả của bất biến chuyển dịch không gian, được thể hiện.

Nói cách khác, những chứng minh này, giờ được gọi là định lý Noether, cho chúng ta biết rằng mỗi khi bạn có một đối xứng vật lý trong hệ thống vật lý của bạn, thì sẽ có một thứ gì đó vật lý liên quan đến hệ thống của bạn được bảo toàn. Có nhiều ví dụ quan trọng mà chúng ta có thể xem xét để minh họa mối liên hệ mạnh mẽ này.

– Nếu hệ thống của bạn đối xứng dưới các phép quay, thì động lượng góc của hệ thống đó sẽ được bảo toàn.

– Nếu hệ thống của bạn bất biến dưới các chuyển dịch không gian (tức là, bạn có thể di chuyển đến bất kỳ vị trí nào và vẫn khôi phục được cùng một hệ thống), thì động lượng tuyến tính của hệ thống đó sẽ được bảo toàn.

– Nếu hệ thống của bạn bất biến dưới các gia tốc (còn được gọi là các biến đổi vận tốc), thì điều đó dẫn đến bảo toàn tứ động lượng: định lý tâm khối lượng.

– Và nếu hệ thống của bạn bất biến dưới các chuyển dịch thời gian (tức là, hệ thống của bạn giống hệt như cách nó đã từng trong quá khứ hoặc sẽ là trong tương lai), thì điều đó dẫn đến năng lượng của hệ thống đó được bảo toàn.

Mục cuối cùng này đặc biệt phù hợp ở đây: nếu hệ thống của bạn không thay đổi theo thời gian – nếu các định luật và thuộc tính của nó không thể phân biệt được dù bạn xem xét nó sớm hơn, muộn hơn, hay ngay bây giờ – thì năng lượng phải được bảo toàn trong đó.

Bảo toàn năng lượng theo chiều thời gian

Nhưng điều ngược lại cũng đúng: nếu vũ trụ tiến hóa theo thời gian, và một ví dụ về sự tiến hóa là khoảng cách giữa hai điểm trong vũ trụ đó thay đổi theo thời gian, thì không có gì đảm bảo rằng năng lượng được bảo toàn cả.

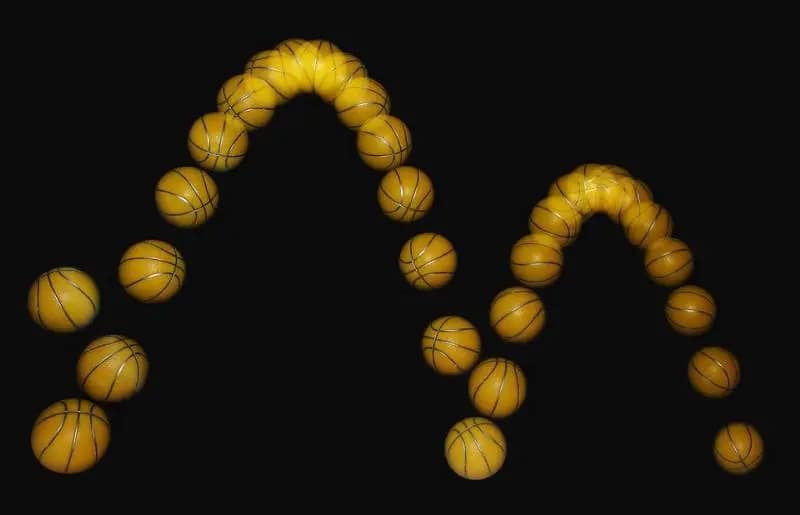
Một quả bóng đang nảy giữa chừng có quỹ đạo quá khứ và tương lai được xác định bởi các định luật vật lý, và chỉ mất năng lượng giữa các lần nảy do các tương tác tiêu tán của quả Программное обеспечение: ball với mặt đất. Người ta không thể biết, dựa trên bức ảnh này, liệu quả bóng nảy sang trái và tăng năng lượng, hay nảy sang phải và mất năng lượng. Nói chung, nếu tất cả các dạng năng lượng được tính đến, năng lượng được bảo toàn cho tất cả bốn tương tác cơ bản trên Trái Đất. Tuy nhiên, trong vũ trụ đang giãn nở, lực hấp dẫn lại có một câu chuyện khác.

Điều này có thể khiến bạn bối rối và khó hiểu. Sau cùng, bảo toàn năng lượng không phải là điều chúng ta nhận ra là một thuộc tính của vũ trụ vì định lý Noether; nó là thứ được phát hiện một cách thực nghiệm: bằng cách định lượng và đo lường tổng lượng năng lượng

– Ban đầu có trong một hệ thống,

– được thêm vào hoặc lấy ra khỏi hệ thống đó,

– và sau đó tồn tại trong hệ thống đó ở trạng thái cuối cùng.

Nếu năng lượng ban đầu, cộng hoặc trừ năng lượng được thêm vào hoặc lấy ra khỏi hệ thống, bằng với lượng năng lượng cuối cùng trong hệ thống, thì bảo toàn năng lượng thực sự được xác nhận. Nếu không, thì bảo toàn năng lượng bị vi phạm.

Đối với các hệ thống phòng thí nghiệm trên Trái Đất, năng lượng thực sự luôn được bảo toàn theo cách chính xác này. Khi bạn cho hai hạt va chạm vào nhau, bất kể cái gì đi vào hay ra khỏi thí nghiệm của bạn, tổng tất cả các năng lượng ban đầu và năng lượng cuối cùng sẽ luôn khớp nhau. Khi bạn thả một hạt trong trường hấp dẫn của Trái Đất, dù bạn bắn nó lên, ném nó ngang, hay để nó rơi, tổng năng lượng của hệ thống hạt – Trái Đất ban đầu và ở cuối sẽ luôn bằng nhau. Thực tế, dưới tất cả bốn tương tác cơ bản – hấp dẫn, điện từ, hoặc thậm chí các lực hạt nhân yếu và mạnh – bất kỳ hệ thống vật lý nào được kiểm tra trên Trái Đất đều luôn được quan sát là bảo toàn năng lượng.

Khi ánh sáng được phát ra từ một nguồn, nó có một bước sóng cụ thể. Ánh sáng phải di chuyển càng lâu qua vũ trụ đang giãn nở trước khi được hấp thụ bởi một người quan sát, thì mức độ dịch chuyển đỏ của bước sóng ánh sáng đó càng lớn, tức là bị kéo dài đến các giá trị dài hơn, so với bước sóng mà nó có khi được phát ra.

Nhưng nếu bạn rời khỏi sân sau vũ trụ của chúng ta, mọi thứ không còn đơn giản như vậy nữa. Nếu bạn chiếu một ánh sáng ra ngoài vũ trụ rộng lớn hơn từ hành tinh Trái Đất, thoạt nhìn có vẻ như năng lượng vẫn được bảo toàn. Khi photon – lượng tử ánh sáng – mà bạn tạo ra bay lên qua bầu khí quyển Trái Đất và vào không gian, nó mất năng lượng, khiến bước sóng của nó dài ra. Tuy nhiên, đây không phải là sự vi phạm bảo toàn năng lượng; năng lượng được bảo toàn vì sự mất năng lượng của photon được cân bằng chính xác bởi sự thay đổi trong năng lượng hấp dẫn khi nó di chuyển xa hơn khỏi tâm Trái Đất.

Quá trình tương tự tiếp tục khi photon rời khỏi Hệ Mặt Trời: nó mất năng lượng (và bước sóng dài ra) khi di chuyển ngày càng xa Mặt Trời và các hành tinh, đổi một sự tăng năng lượng tiềm năng hấp dẫn (leo ra khỏi giếng thế năng hấp dẫn) để lấy một sự mất năng lượng động lực của photon. Khi photon thoát khỏi lực kéo hấp dẫn của Dải Ngân Hà, điều tương tự xảy ra: sự mất năng lượng trong năng lượng động lực của photon được cân bằng bởi năng lượng tiềm năng hấp dẫn mà nó thu được khi rời khỏi trường hấp dẫn của vật thể mà nó bắt nguồn. Điều này tiếp tục cho đến khi nó thoát khỏi Nhóm Địa phương, đó là lần cuối cùng tổng năng lượng được bảo toàn.

Tuy nhiên, một khi photon tiến vào không gian liên thiên hà thực sự, câu chuyện thay đổi đáng kể. Khi nó di chuyển qua vũ trụ, giờ đây nó mất năng lượng, mà không có dạng năng lượng nào khác trải qua sự tăng năng lượng tương ứng.

Khi cấu trúc của vũ trụ giãn nở, các bước sóng của bất kỳ bức xạ nào hiện diện cũng sẽ bị kéo dài. Trong một cấu trúc liên kết, như một hệ thống sao, thiên hà, hoặc nhóm thiên hà, không gian không giãn nở, nhưng giữa các cấu trúc liên kết, trong không gian liên thiên hà sâu thẳm, không gian thực sự giãn nở. Sự kéo dài bước sóng này (và sự mất năng lượng) áp dụng cho cả sóng hấp dẫn và sóng vật chất (sóng de Broglie) cũng như cho sóng điện từ; bất kỳ dạng bức xạ nào cũng có bước sóng bị kéo dài khi vũ trụ giãn nở.

Chuyện gì đang xảy ra ở đây?

Một khi một photon – hoặc bất kỳ dạng năng lượng nào, về vấn đề đó – rời khỏi Nhóm Địa phương của các thiên hà, nó không còn là một phần của một cấu trúc liên kết (bởi lực hấp dẫn). Thay vào đó, nó chỉ di chuyển qua không gian: qua không gian giãn nở của vũ trụ rộng lớn hơn. Sau tất cả, chúng ta đã biết trong khoảng 100 năm rằng vũ trụ đang giãn nở, như đã được dự đoán về mặt lý thuyết và đo lường qua quan sát vào những năm 1920. Khi vũ trụ giãn nở, khoảng cách giữa bất kỳ hai điểm nào trở nên lớn hơn theo thời gian, bao gồm cả hai điểm xác định kích thước của một bước sóng cho bất kỳ photon riêng lẻ nào, hay lượng tử ánh sáng.

Nói cách khác, khi vũ trụ giãn nở và một photon di chuyển qua nó, bước sóng của nó kéo dài đến các bước sóng ngày càng dài hơn, điều này lần lượt đưa nó đến các năng lượng ngày càng thấp hơn. (Năng lượng của một photon được xác định bởi bước sóng của nó!) Lần này, năng lượng không đi đâu cả; năng lượng cuối cùng chỉ đơn giản là khác với năng lượng ban đầu vì năng lượng không được bảo toàn trong vũ trụ đang giãn nở. Sau tất cả, nếu không có đối xứng chuyển dịch thời gian, thì không có đại lượng bảo toàn tương ứng của năng lượng, và một vũ trụ giãn nở (hoặc co lại, về vấn đề đó) về cơ bản là khác – đặc biệt về mặt khoảng cách phân tách bất kỳ hai điểm nào – từ khoảnh khắc này sang khoảnh khắc tiếp theo.

Đối với bức xạ di chuyển qua một vũ trụ đang giãn nở, năng lượng không được bảo toàn; nó bị mất.

Vũ trụ giãn nở

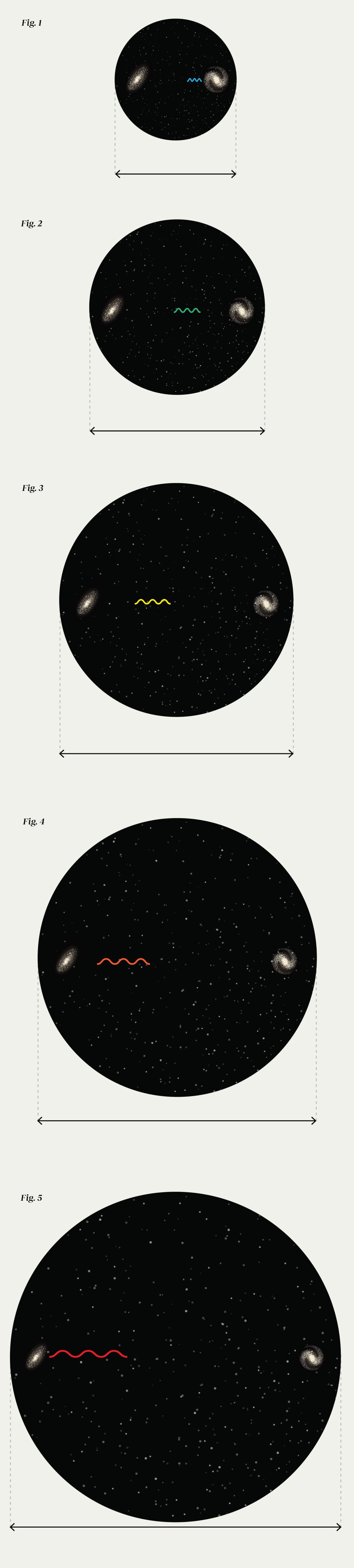
Hình ảnh động đơn giản hóa này cho thấy ánh sáng bị dịch chuyển đỏ như thế nào và khoảng cách giữa các vật thể không liên kết thay đổi theo thời gian trong vũ trụ đang giãn nở. Lưu ý rằng các vật thể bắt đầu gần nhau hơn so với thời gian ánh sáng cần để di chuyển giữa chúng, ánh sáng bị dịch chuyển đỏ do sự giãn nở của không gian, và hai thiên hà cuối cùng cách nhau xa hơn nhiều so với đường đi ánh sáng của photon được trao đổi giữa chúng.

Nhưng bức xạ không phải là loại năng lượng duy nhất được phép hiện diện trong vũ trụ của chúng ta. Còn có vật chất (cả thông thường và tối), neutrino (hành xử như bức xạ khi chúng có nhiều năng lượng động lực và hành xử như vật chất khi chúng có rất ít), các khuyết tật topo (như dây vũ trụ và tường miền, có thể chỉ là lý thuyết), và năng lượng vốn có trong cấu trúc của chính không gian. Dạng năng lượng cuối cùng này xuất hiện dưới nhiều hình thức khác nhau.

– Một hằng số vũ trụ, được biết đến là Λ trong thuyết tương đối tổng quát của Einstein, hành xử như một dạng năng lượng vốn có trong không gian.

– Năng lượng chân không của lý thuyết trường lượng tử, còn được gọi là năng lượng điểm không của không gian, hành xử như năng lượng vốn có trong không gian.

– Năng lượng tối, thứ thúc đẩy sự giãn nở gia tốc hiện đại của vũ trụ ngày nay, là một dạng năng lượng vốn có trong không gian.

– Và vào thời kỳ đầu của lịch sử vũ trụ, trong một giai đoạn lạm phát vũ trụ trước và thiết lập nên Vụ Nổ Lớn nóng, năng lượng vốn có trong không gian là rất lớn, và thúc đẩy vũ trụ giãn nở với tốc độ cấp số nhân: tăng gấp đôi kích thước trong cả ba chiều với mỗi phần nhỏ của giây trôi qua, trong khi mật độ năng lượng của nó vẫn không đổi.

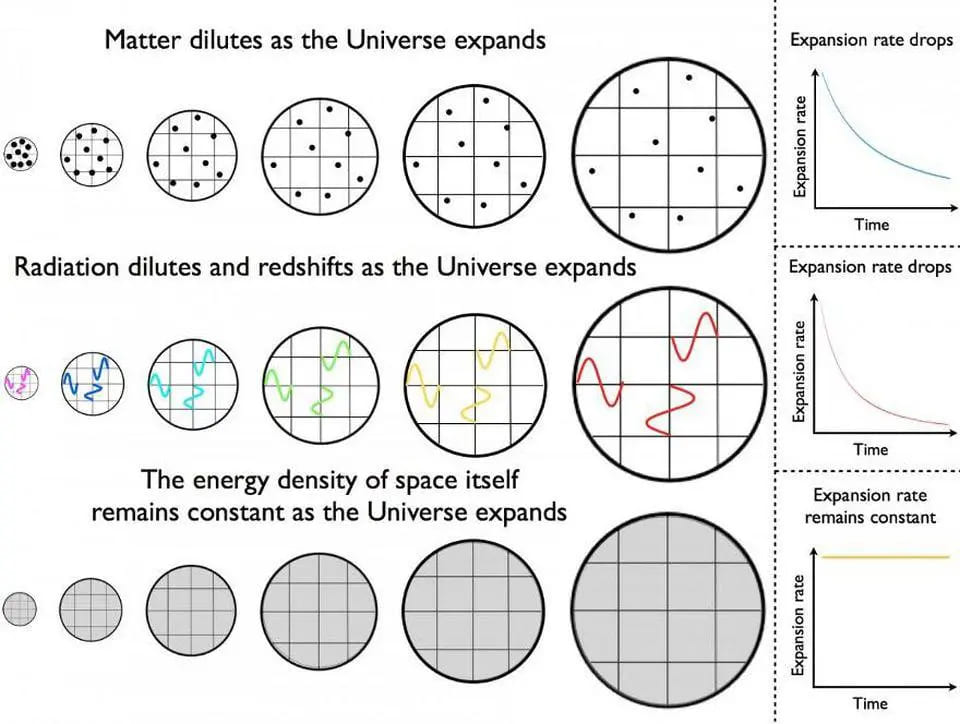
Đó là đặc điểm chính của một vũ trụ có năng lượng vốn có trong không gian: khi nó giãn nở, không gian mới được tạo ra, nhưng mật độ năng lượng vẫn không đổi. Cùng mật độ nhưng khối lượng lớn hơn có nghĩa là tổng năng lượng tăng lên, tổng thể. Trong khi một vũ trụ chứa đầy bức xạ (tức là, một vũ trụ chứa đầy photon) mất năng lượng khi nó giãn nở, một vũ trụ chứa đầy năng lượng vốn có trong không gian (tức là, vũ trụ đang lạm phát) lại tăng năng lượng khi nó giãn nở.

Cách mà vật chất (trên cùng), bức xạ (giữa), và năng lượng tối/năng lượng lạm phát (dưới cùng) tiến hóa theo thời gian trong một vũ trụ đang giãn nở. Khi vũ trụ giãn nở, mật độ vật chất loãng ra, nhưng bức xạ cũng trở nên mát hơn khi các bước sóng của nó bị kéo dài đến các trạng thái dài hơn, ít năng lượng hơn. Mật độ của năng lượng tối (hoặc năng lượng lạm phát), mặt khác, sẽ thực sự giữ nguyên nếu nó hành xử như hiện được nghĩ: như một dạng năng lượng vốn có trong chính không gian. Tổng năng lượng trong một vùng không gian đang giãn nở không được bảo toàn.

Đây không phải là một lỗi; đây là thứ bắt buộc trong vũ trụ đang giãn nở của chúng ta. Vì không có đối xứng chuyển dịch thời gian – vì vũ trụ ở bất kỳ khoảnh khắc nào cũng khác với vũ trụ ở khoảnh khắc trước hoặc sau đó – năng lượng không được bảo toàn chút nào. Thật hấp dẫn để nói rằng, tùy thuộc vào loại hoặc loài năng lượng hiện diện trong vũ trụ, tổng năng lượng là thứ có thể giảm (như đối với bức xạ) hoặc tăng (như đối với năng lượng lạm phát), nhưng một phát biểu trung thực hơn sẽ là năng lượng thậm chí không được xác định rõ trong một vũ trụ không có đối xứng chuyển dịch thời gian. Trong một vũ trụ đang giãn nở, không có định nghĩa nhất quán về năng lượng chút nào.

Tại sao không thể xác định năng lượng trong một vũ trụ không có đối xứng chuyển dịch thời gian, như trong một vũ trụ đang giãn nở?

Hãy xem xét một so sánh với điện từ học. Khi các vật mang điện tích di chuyển xa nhau, ví dụ, đó là vì hoặc một lực bảo toàn (như lực điện) đang đẩy chúng ra xa nhau, hoặc một lực bên ngoài được áp dụng qua một khoảng cách, thực hiện công trên các hạt đó để di chuyển chúng. Vì công chỉ là một dạng năng lượng khác, và vì các lực bằng và ngược lại tác động lên các điện tích này bảo toàn tổng năng lượng (động lực + thế năng điện), dễ thấy rằng bảo toàn năng lượng vẫn được giữ. Nhưng đối với lực hấp dẫn, mọi thứ (bao gồm những thứ có khối lượng và, hoặc năng lượng) có thể di chuyển xa nhau vì có một lực bảo toàn (như một sao chổi định kỳ rời xa Mặt Trời), hoặc chúng có thể di chuyển xa nhau vì chính cấu trúc của không gian đang thực sự giãn nở.

Cả bên trong và bên ngoài chân trời sự kiện của một lỗ đen Schwarzschild, không gian chảy như một lối đi di động hoặc một thác nước, tùy thuộc vào cách bạn muốn hình dung nó. Không giống như trường hợp của một vũ trụ đang giãn nở, trường hợp của một khối lượng điểm không quay trong không gian – thời gian, tạo ra một lỗ đen Schwarzschild, là một giải pháp không gian – thời gian tĩnh với đối xứng chuyển dịch thời gian. Trong không gian – thời gian này, tất cả các lực đều là bảo toàn và năng lượng, cũng vậy, luôn được bảo toàn.

Trong trường hợp đầu tiên, của một sao chổi quay quanh Mặt Trời, những thay đổi trong khoảng cách và tốc độ của hệ thống sao chổi – Mặt Trời dẫn đến năng lượng được bảo toàn, vì tổng năng lượng ban đầu và tổng năng lượng cuối cùng sẽ bằng nhau. Nhưng trong trường hợp thứ hai, của một vũ trụ đang giãn nở, không có cách tốt để xác định tổng năng lượng của hệ thống là gì, vì không có khung tham chiếu khách quan, không thay đổi để xác định nó.

Vì chúng ta có thể quan sát và đo lường rằng vũ trụ đang giãn nở, điều đó có nghĩa là các vị trí và khoảng cách tương đối thay đổi theo thời gian. Do đó, bất kỳ đại lượng phụ thuộc năng lượng nào phụ thuộc vào lượng khoảng cách hoặc không gian mà các vật thể chiếm giữ, bao gồm các đại lượng như bước sóng, năng lượng tiềm năng hấp dẫn, và khối lượng không gian (với mật độ năng lượng dương, không đổi trong suốt lạm phát) được bao bọc trong vũ trụ có thể quan sát cũng thay đổi.

Mọi người thường hỏi liệu việc giãn nở vũ trụ có tốn năng lượng không, hoặc liệu chúng ta có thể thu được năng lượng nếu vũ trụ ngừng giãn nở và bắt đầu co lại. Nhưng điều này giả định rằng tách các vật thể có năng lượng là một việc tốn năng lượng ngay từ đầu; điều đó chỉ đúng trong một vũ trụ không giãn nở, không co lại! Sự giãn nở của không gian là miễn phí theo nghĩa nó không tốn bất kỳ năng lượng nào cả; nó xảy ra theo thời gian, miễn phí, như một hệ quả tất yếu của vũ trụ đang giãn nở.

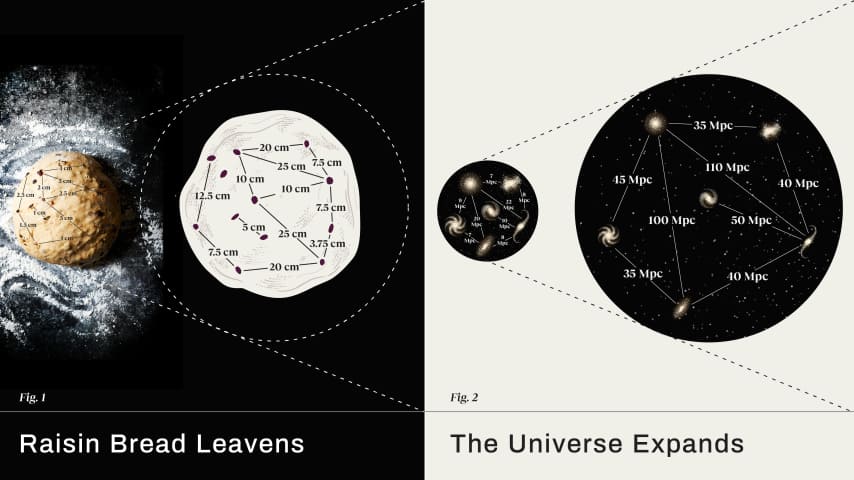
Mô hình bánh mì nho khô của vũ trụ đang giãn nở, nơi các khoảng cách tương đối tăng lên khi không gian (bột bánh) giãn nở. Hai quả nho khô càng ở xa nhau, thì mức độ dịch chuyển đỏ quan sát được sẽ càng lớn vào thời điểm ánh sáng được nhận. Sự giãn nở này khiến mật độ bức xạ giảm và năng lượng trên mỗi photon giảm, nhưng cho phép mật độ năng lượng tối giữ nguyên. Sự kết hợp này có thể làm tăng hoặc giảm tổng năng lượng mà người ta sẽ tính toán cho vũ trụ có thể quan sát, rõ ràng là vi phạm bảo toàn năng lượng.

Thật buồn cười, khi bạn nghĩ về nó, rằng đây là một trường hợp rất, rất quan trọng nơi câu nói cũ không có bữa ăn trưa miễn phí không áp dụng. Khi vũ trụ giãn nở với tốc độ cấp số nhân – cả trong suốt lạm phát vào thời kỳ đầu và trong thời kỳ năng lượng tối thống trị vào thời kỳ sau – có một thứ bạn nhận được miễn phí: những lượng không gian bổ sung. Không gian trống, trong những điều kiện này, không tốn gì cả; khi nó được tạo ra, nó đi kèm với cùng mật độ năng lượng mà không gian tạo ra nó cũng có.

Liệu điều đó có nghĩa là chúng ta nhận được năng lượng miễn phí từ việc lạm phát, hay bất kỳ không gian nào giãn nở theo cấp số nhân?

Tôi sẽ không nhìn nhận theo cách đó; năng lượng toàn cầu không phải là thứ được xác định rõ cho một vũ trụ đang giãn nở. Thực tế, nếu bạn không có đối xứng chuyển dịch thời gian cho vũ trụ của bạn – bao gồm cả cho không gian – thời gian của bạn dưới thuyết tương đối của Einstein – điều đó đảm bảo rằng năng lượng không được bảo toàn.

Có thể xác định áp suất, công, và năng lượng theo cách mà mỗi vùng không gian giãn nở thực hiện công âm lên môi trường xung quanh, với năng lượng tối thực hiện công với áp suất P =– ρc². Tuy nhiên, đây là một định nghĩa tùy tiện, không phải là một định nghĩa được áp đặt bởi các phương trình. Trong thực tế của vũ trụ đang giãn nở, năng lượng toàn cầu không chỉ không được bảo toàn, mà còn không được xác định.

Thật hấp dẫn để cố gắng xác định lại năng lượng theo cách bao gồm công được thực hiện bởi một vùng không gian lên môi trường xung quanh, cả ở dạng dương (ví dụ, từ bức xạ) và dạng âm (ví dụ, từ năng lượng tối). Nhưng điều duy nhất bạn thu được từ đó là sự hài lòng cá nhân từ việc nghĩ ra một định nghĩa cho phép thứ mới này vẫn được bảo toàn trong vũ trụ đang giãn nở; tuy nhiên, không có gì hữu ích, có thể khai thác, hoặc áp dụng được từ nó. Nó không hành xử như năng lượng theo nghĩa thông thường; đó chỉ là một sự xác định lại được thúc đẩy bởi cảm giác thẩm mỹ thiên vị của chúng ta.

Lạm phát vũ trụ thực sự vi phạm bảo toàn năng lượng, nhưng không phải vì có gì đặc biệt về năng lượng tối hay một không gian – thời gian giãn nở theo cấp số nhân: với mật độ năng lượng không đổi. Miễn là không gian – thời gian của bạn thiếu đối xứng chuyển dịch thời gian, bảo toàn năng lượng bị vi phạm. Hơn nữa, một định nghĩa năng lượng không thể xác định một cách chặt chẽ trong những điều kiện như vậy. Các đối xứng đóng một vai trò quan trọng trong vật lý, nhưng có nhiều đối xứng mà vũ trụ của chúng ta đơn giản là không hiển thị. Miễn là vũ trụ của bạn giãn nở, co lại, hoặc thay đổi theo thời gian, năng lượng cũng sẽ không được bảo toàn ở đó.