Lịch sử mật mã, từ người Sparta đến FBI

Nhà khoa học máy tính Panos Louridas truy dấu sự phát triển của truyền thông bí mật, từ Hy Lạp cổ đại đến kỷ nguyên lượng tử.

Khi Chiến dịch Trojan Shield kết thúc vào ngày 8 tháng 6 năm 2021, kết quả thật đáng kinh ngạc: Hơn 800 vụ bắt giữ diễn ra tại 16 quốc gia, gần 40 tấn ma túy bị thu giữ, cùng với 250 khẩu súng, 55 chiếc xe sang, và hơn 48 triệu đô la tiền mặt cùng tiền điện tử.

Trung tâm của chiến dịch – một trong những chiến dịch lớn nhất thuộc loại này – là một ứng dụng nhắn tin độc quyền có tên ANOM. Ứng dụng này, được quảng cáo như một nền tảng liên lạc an toàn dựa trên mã hóa, cung cấp các tính năng vượt trội so với các thiết bị thông thường, chẳng hạn như khả năng xóa toàn bộ tin nhắn và dữ liệu từ xa trên điện thoại bị bắt giữ, qua đó tiêu hủy mọi bằng chứng buộc tội.

Vấn đề đối với người dùng là ANOM thực chất do FBI điều hành. Các cơ chế bảo vệ quyền riêng tư chỉ là vỏ bọc: Tất cả các cuộc trao đổi đều bị sao chép và chuyển tiếp đến các cơ quan chính phủ tham gia chiến dịch. Theo Europol – cơ quan thực thi pháp luật của Liên minh châu Âu, 27 triệu tin nhắn đã được thu thập từ hơn 100 quốc gia.

Ảo tưởng về sự bảo mật và riêng tư trong liên lạc này phản ánh vai trò sâu xa hơn của mật mã trong thế giới kỹ thuật số hiện đại. Chiến dịch này làm nổi bật cả sức mạnh lẫn điểm yếu của mã hóa, vốn đã đóng vai trò trung tâm trong truyền thông bảo mật suốt nhiều thế kỷ. Đúng vậy, nhiều thế kỷ. Mật mã – nghệ thuật mã hóa và giải mã thông tin bí mật – có nguồn gốc từ Hy Lạp cổ đại.

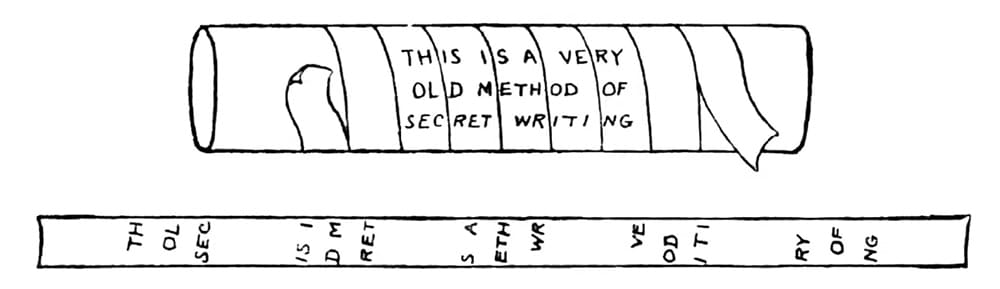
Thuật ngữ cryptography bắt nguồn từ tiếng Hy Lạp với nghĩa chữ viết ẩn, và lịch sử mật mã có thể truy nguyên về người Sparta. Theo Plutarch, họ sử dụng một công cụ gọi là scytale hay skytale (từ tiếng Hy Lạp σκυτάλη, nghĩa là cây gậy hoặc trụ tròn) để che giấu thông điệp. Công cụ này bao gồm một thanh trụ, quanh đó quấn một dải da hoặc giấy da. Thông điệp sẽ được viết lên dải này khi nó được quấn quanh scytale, và sau đó được gửi đi mà không có thanh trụ. Để đọc được thông điệp, người nhận cần có một scytale có hình dạng giống hệt; nếu không, những chữ cái sẽ trở nên vô nghĩa.

Mật mã trong đế chế La Mã

Người La Mã cũng sử dụng mật mã. Nhà sử học Suetonius ở thế kỷ thứ nhất đã viết về Julius Caesar:

Nếu ông ta có điều gì cần giữ bí mật, ông ta sẽ viết nó bằng mật mã, tức là thay đổi thứ tự các chữ cái trong bảng chữ cái sao cho không ai có thể hiểu được. Nếu ai đó muốn giải mã và hiểu ý nghĩa của nó, người đó phải thay thế chữ cái thứ tư trong bảng chữ cái, cụ thể là chữ D thay cho A, và tương tự đối với các chữ cái khác.

Suetonius đang mô tả mật mã Caesar, một dạng mật mã thay thế, có nghĩa là nó hoạt động bằng cách thay thế các chữ cái trong bảng chữ cái bằng những chữ cái khác. Để đọc được một tin nhắn được mã hóa bằng mật mã Caesar, bạn cần biết khóa – số vị trí mỗi chữ cái bị dịch chuyển (trong trường hợp trên là bốn). Nếu không biết khóa, bạn có thể thử từng giá trị cho đến khi tìm ra giá trị đúng. Trong tiếng Anh, tối đa bạn chỉ cần thử 25 lần dịch chuyển khác nhau.

Một lựa chọn tốt hơn có thể là xáo trộn bảng chữ cái và quyết định thay thế, chẳng hạn, D cho A, C cho B, và cứ thế tiếp tục. Để giải mã tin nhắn đó, chúng ta chỉ cần một bảng ánh xạ:

Việc thử tất cả các bảng ánh xạ có thể là một ý tưởng, nhưng sẽ nhanh chóng trở nên bất khả thi. Có hơn 400 septillion (tức là một con số có 27 chữ số thập phân!) bảng ánh xạ khác nhau!

Phá mã và trò chơi mèo vờn chuột trong mật mã học

Khi chúng ta cố gắng phá một phương pháp mã hóa hoặc đọc một thông điệp được mã hóa bằng cách thử tất cả các khả năng khác nhau, chúng ta đang sử dụng phương pháp tấn công vét cạn (brute force). Tuy nhiên, tấn công vét cạn hiếm khi là phương pháp hiệu quả nhất. Một phương pháp giải mã nền tảng – và hiệu quả hơn – được gọi là phân tích tần số, lần đầu tiên được mô tả bởi học giả và nhà khoa học Ả Rập thế kỷ thứ chín, Abu Yūsuf Yaʻqūb ibn ‘Isḥāq aṣ-Ṣabbāḥ al-Kindī (801 – 873), còn được biết đến với tên gọi al Kindi.

Tất cả các ngôn ngữ đều có quy luật nhất định, và trong mọi ngôn ngữ, các chữ cái xuất hiện với xác suất khác nhau. Trong tiếng Anh, chữ cái xuất hiện nhiều nhất là E; chữ phổ biến thứ hai là T; chữ ít xuất hiện nhất là Z. Do đó, ký tự xuất hiện nhiều nhất trong một văn bản mã hóa rất có thể là E. Ký tự xuất hiện nhiều thứ hai có thể là T. Và cứ thế tiếp tục. Điều này có nghĩa là chỉ với một chút thống kê và phỏng đoán, chúng ta có thể tránh được việc phải thử mọi khả năng và giải mã thông điệp.

Trò chơi mèo vờn chuột này đã định hình mật mã học trong nhiều thế kỷ. Một phương pháp mã hóa mới được phát minh và được cho là an toàn, nhưng sau đó lại bị phá giải. Sau một thời gian, một phương pháp tốt hơn được phát minh và được xem là bất khả xâm phạm trước các cuộc tấn công đã biết. Và chu kỳ cứ tiếp tục lặp lại.

Sự tiến hóa của các phương pháp mật mã

Sự phát triển trong kỹ thuật mã hóa đã thúc đẩy sự ra đời của các phương pháp ngày càng tinh vi hơn. Một bước tiến quan trọng là sự chuyển đổi từ mật mã đơn bảng (monoalphabetic cipher), như mật mã thay thế đã đề cập ở trên, sang mật mã đa bảng (polyalphabetic cipher), sử dụng nhiều quy tắc thay thế khác nhau để tăng cường bảo mật.

Để mã hóa một thông điệp bằng mật mã đa bảng, chúng ta không sử dụng một bảng ánh xạ duy nhất mà sử dụng nhiều bảng. Chữ cái đầu tiên được mã hóa bằng bảng thứ nhất, chữ cái thứ hai bằng bảng thứ hai, và cứ tiếp tục cho đến bảng cuối cùng; sau đó, chúng ta quay lại bảng đầu tiên và lặp lại chu trình. Khi quy tắc ánh xạ thay đổi, cùng một chữ cái sẽ không luôn luôn được mã hóa theo cùng một cách: tại một vị trí trong thông điệp, A có thể được ánh xạ thành K, nhưng ở vị trí khác lại thành X. Điều này khiến cho phương pháp phân tích tần số đơn giản không thể hoạt động được.

Một trong những dạng phát triển cao hơn của mật mã đa bảng là mật mã Vigenère, tồn tại mà không bị phá giải trong suốt ba thế kỷ cho đến năm 1863.

Thực tế, mật mã Vigenère – được đặt theo tên Blaise de Vigenère (1523 – 1596), nhưng thực chất được phát minh bởi Giovan Battista Bellaso vào năm 1553 – đã không bị phá giải trong ba thế kỷ, cho đến năm 1863. Nó từng được gọi là le chiffrage indéchiffrable (tiếng Pháp có nghĩa là mật mã không thể phá giải).

Cuối cùng, mật mã Vigenère đã bị phá vỡ bởi Friedrich Kasiski, một sĩ quan bộ binh, nhà mật mã học và nhà khảo cổ học người Đức. Ông nhận ra rằng phân tích tần số vẫn có thể được áp dụng bằng cách xác định số lượng bảng ánh xạ khác nhau được sử dụng, cho phép tách các đoạn thông điệp được mã hóa bằng cùng một bảng ánh xạ để phân tích riêng biệt.

Đỉnh cao của mật mã học cổ điển – Máy Enigma

Điểm đỉnh của trò chơi mèo vờn chuột trong mật mã học cổ điển chính là máy Enigma, được quân đội Đức sử dụng trong Thế Chiến II. Máy Enigma là một hệ thống mã hóa đa bảng cực kỳ phức tạp, và phải mất nhiều năm nỗ lực của các nhà giải mã Ba Lan và Anh, cùng với thiên tài tiên phong trong khoa học máy tính Alan Turing, mới có thể phá giải nó.

Câu chuyện về Enigma đã trở thành huyền thoại. Đây là một cột mốc quan trọng: Lần đầu tiên, việc giải mã không còn do các nhà ngôn ngữ học hay những người đam mê giải đố thực hiện, mà do các nhà toán học đảm nhiệm. Để phá mã Enigma, Alan Turing đã thiết kế một cỗ máy mang tên Bombe, hiện đã được phục dựng một cách tỉ mỉ tại Bletchley Park, nơi nó từng được chế tạo trong chiến tranh. Máy móc đã được sử dụng để phá giải mã hóa do máy móc tạo ra. Và từ đó trở đi, đây trở thành xu hướng tất yếu của mật mã học.

Chuẩn mật mã thống trị thế giới số ngày nay – AES

Ngày nay, một thuật toán mã hóa đóng vai trò nền tảng cho hạ tầng kỹ thuật số của chúng ta là Chuẩn mã hóa tiên tiến (AES – Advanced encryption standard). AES được phát triển bởi hai nhà mật mã học người Bỉ, Joan Daemen và Vincent Rijmen, và được Viện Tiêu chuẩn và Công nghệ Quốc gia Hoa Kỳ (NIST) chấp nhận vào năm 2001 sau một quá trình đánh giá kéo dài năm năm với nhiều đề xuất cạnh tranh.

AES hoạt động bằng cách liên tục thực hiện các phép thay thế và hoán vị các ký tự trong văn bản, dựa trên các nguyên lý toán học, đặc biệt là lý thuyết số – lĩnh vực nghiên cứu về số nguyên. Nếu không có khóa giải mã chính xác, việc giải mã một thông điệp được mã hóa bằng AES là gần như không thể.

Là một hệ thống mã hóa đối xứng, AES sử dụng cùng một khóa cho cả việc mã hóa và giải mã, giống như các hệ thống mã hóa mà chúng ta đã đề cập trước đó. Tuy nhiên, sự đối xứng này tạo ra một vấn đề: Người gửi và người nhận phải trao đổi khóa, và họ không thể mã hóa chính khóa đó, vì điều này sẽ yêu cầu một khóa khác. Vậy họ giải quyết vấn đề này như thế nào?

Đột phá của Diffie Hellman – Cách chia sẻ khóa mã hóa an toàn

Năm 1976, hai nhà mật mã học người Mỹ Whitfield Diffie và Martin Hellman đã công bố một bài báo thay đổi hoàn toàn mật mã học. Trong bài báo này, họ mô tả phương pháp trao đổi khóa Diffie Hellman, một kỹ thuật cho phép hai bên thiết lập một khóa dùng chung một cách an toàn mà không cần gặp mặt hoặc trao đổi riêng tư.

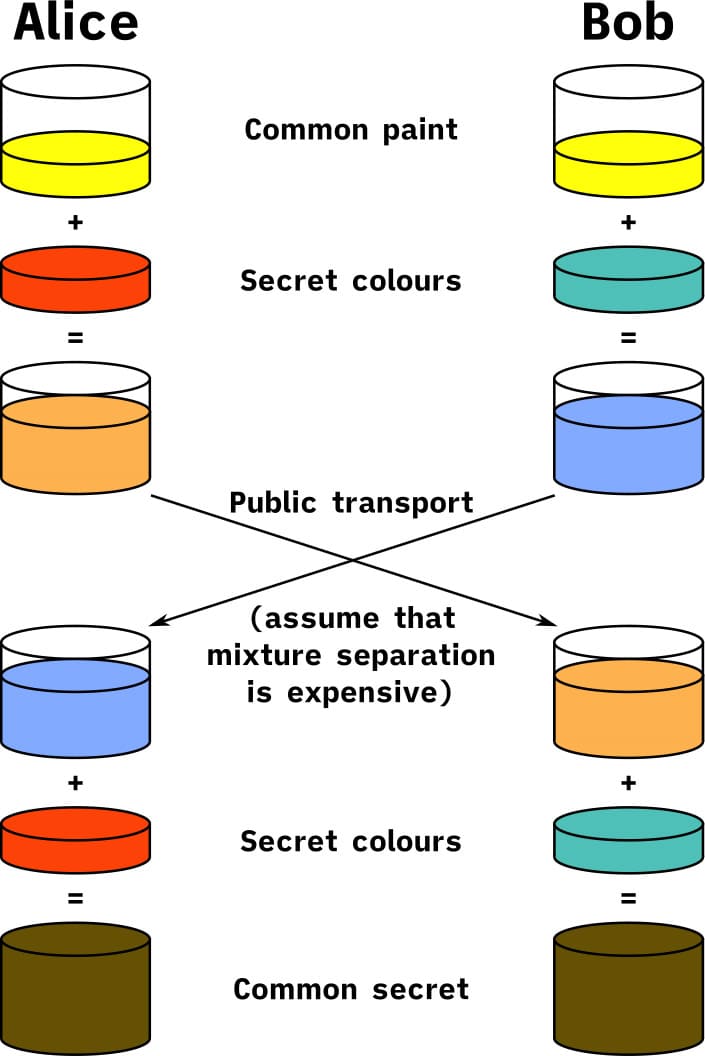
Có một cách minh họa phổ biến để giúp dễ hình dung về phương pháp trao đổi khóa Diffie Hellman, thay thế toán học bằng màu sắc:

Giả sử Alice và Bob cùng đồng ý về một màu nền chung, chẳng hạn như màu vàng. Mỗi người sau đó chọn một màu bí mật và trộn nó với màu vàng. Alice gửi hỗn hợp màu của mình cho Bob, và Bob cũng gửi hỗn hợp màu của mình cho Alice. Khi nhận được hỗn hợp của đối phương, mỗi người lại thêm vào màu bí mật của chính mình. Kết quả cuối cùng là cả Alice và Bob đều có cùng một màu cuối cùng.

Một bên thứ ba có thể biết màu vàng ban đầu và các màu trung gian, nhưng họ không thể dễ dàng tái tạo màu cuối cùng. Đây chính là nguyên lý đằng sau trao đổi khóa Diffie Hellman – một bước tiến cách mạng trong lĩnh vực mật mã học.

Trên thực tế, phương pháp Diffie Hellman không sử dụng màu sắc mà sử dụng những con số cực kỳ lớn. Tính bảo mật của nó phụ thuộc vào độ khó trong việc đảo ngược quá trình – giống như cách chúng ta không thể dễ dàng tách các màu sơn đã trộn lẫn, một kẻ nghe lén cũng không thể tính toán được khóa bí mật chung mà không biết các số riêng tư.

Ít nhất, đây là điều mà các nhà mật mã học tin tưởng. Hiện chưa có chứng minh toán học nào khẳng định rằng việc suy ra khóa chung là bất khả thi (tương tự như việc không thể tách màu đã trộn). Để làm được điều đó, cần phải giải quyết vấn đề được gọi là bài toán logarit rời rạc. Hiện tại, chưa có phương pháp hiệu quả nào để giải bài toán này, và nhiều người tin rằng sẽ không có phương pháp nào được phát hiện trong tương lai.

Đây chính là tình trạng điển hình trong mật mã học hiện đại: Chúng ta tin rằng một hệ mã hóa là an toàn vì tính bảo mật của nó phụ thuộc vào việc giải một bài toán toán học, mà cho đến nay, dù đã cố gắng hết sức, chúng ta vẫn chưa tìm ra lời giải.

RSA và sự ra đời của mật mã khóa công khai

Một bước đột phá khác xuất hiện vào năm 1978 khi ba nhà nghiên cứu Ron Rivest, Adi Shamir và Leonard Adleman phát minh ra hệ mã hóa RSA (được đặt tên theo chữ cái đầu của họ), mở ra kỷ nguyên của mật mã khóa công khai.

Trong một hệ mã khóa công khai, có một khóa công khai và một khóa bí mật tương ứng. Khóa công khai có thể được sử dụng để mã hóa một thông điệp, nhưng chỉ có khóa bí mật mới có thể giải mã nó. Vì khóa công khai không cần được giữ bí mật, nếu Alice muốn gửi một thông điệp an toàn cho Bob, cô ấy có thể lấy khóa công khai của Bob từ một kênh công khai bất kỳ và sau đó sử dụng nó để mã hóa thông điệp.

Tính bảo mật của hệ mã RSA dựa trên độ khó của việc phân tích một số nguyên thành tích của các số nguyên tố nhỏ hơn. Ví dụ, 60 = 2 × 2 × 3 × 5. Quá trình này, được gọi là phân tích thừa số nguyên tố, rất khó thực hiện nhanh đối với những số lớn. Trong mật mã học, chúng ta sử dụng những con số cực kỳ lớn để đảm bảo tính an toàn.

Mật mã khóa đối xứng vẫn chưa bị lỗi thời

Mặc dù mật mã khóa công khai mở ra những chân trời mới, nhưng mật mã khóa đối xứng vẫn chưa hề lỗi thời, vì nó nhanh hơn đáng kể. Trên thực tế, mật mã khóa công khai thường được sử dụng để trao đổi khóa – như trong giao thức Diffie Hellman – cho phép hai bên thiết lập một khóa bí mật chung một cách an toàn. Sau đó, khóa này sẽ được sử dụng cho phương pháp mã hóa đối xứng hiệu quả hơn.

Ngoài việc mã hóa thông điệp, mật mã khóa công khai còn cho phép tạo chữ ký số. Nếu Alice mã hóa một thông điệp bằng khóa bí mật của cô ấy, thì chỉ những người có khóa công khai của cô ấy mới có thể giải mã nó. Điều này đảm bảo tính xác thực, vì chỉ có Alice mới có thể mã hóa thông điệp bằng khóa bí mật của cô ấy.

Quá trình trao đổi khóa và mã hóa đối xứng diễn ra liên tục trên các thiết bị kỹ thuật số của chúng ta. Khi chúng ta bắt đầu một phiên giao tiếp, dù là truy cập một trang web hay thiết lập một cuộc gọi video hoặc âm thanh, thiết bị của chúng ta sẽ trao đổi một khóa bí mật với bên đối tác.

Sau khi khóa này được thiết lập, mọi thông tin liên lạc sẽ được mã hóa bằng một cơ chế mã hóa đối xứng như AES. Tất cả những điều này diễn ra hoàn toàn tự động, nhanh đến mức chúng ta không nhận thấy bất kỳ độ trễ nào. Nhưng nếu không có nó, không có hình thức giao tiếp số nào mà chúng ta biết sẽ còn an toàn.

Mối đe dọa từ máy tính lượng tử

Tuy nhiên, trò chơi mèo vờn chuột vẫn chưa kết thúc. Ngày nay, mật mã học đang đối mặt với một thách thức lớn: máy tính lượng tử.

Khi trở nên thực tiễn, máy tính lượng tử có thể giải quyết một số bài toán nhanh hơn rất nhiều so với máy tính ngày nay, khiến các hệ thống như RSA và Diffie Hellman trở nên không còn an toàn.

Hiện tại, máy tính lượng tử vẫn chưa đạt đến mức có thể đe dọa các công cụ mật mã của chúng ta, nhưng điều đó không có nghĩa là các nhà mật mã học không có hành động gì.

Một lĩnh vực nghiên cứu mới đã bắt đầu: mật mã hậu lượng tử. Đây là các phương pháp mật mã mà, theo hiểu biết hiện tại, sẽ không bị tổn thương trước các cuộc tấn công của máy tính lượng tử.

Mật mã hậu lượng tử không chỉ nhằm bảo vệ quyền riêng tư trong tương lai mà còn bảo vệ dữ liệu ngày nay. Hãy tưởng tượng một kịch bản trong đó ai đó lưu trữ các cuộc trao đổi của chúng ta với ý định giải mã chúng khi máy tính lượng tử trở nên khả thi. Chiến lược này, được gọi là lưu trữ ngay bây giờ, giải mã sau này, có thể đe dọa những bí mật cần phải được giữ an toàn trong cả ngắn hạn và dài hạn.

Tương tự như cách mà chuẩn mã hóa AES được phát triển trong tinh thần minh bạch, quá trình phát triển mật mã hậu lượng tử cũng đang diễn ra một cách công khai. Nhiều đề xuất khác nhau đang được đánh giá để được Viện Tiêu Chuẩn và Công Nghệ Quốc Gia Hoa Kỳ (NIST) chấp nhận làm tiêu chuẩn.

Sự phát triển của mật mã học, xét cho cùng, là một chu kỳ liên tục của những đột phá và thất bại, có lẽ được mô tả tốt nhất qua câu nói của Samuel Beckett: Try Again. Fail Again. Fail Better.

Giới thiệu tác giả Panos Louridas

Panos Louridas là giáo sư tại Khoa Khoa Học Quản Lý và Công Nghệ, Trường Đại Học Kinh Tế và Kinh Doanh Athens. Ông là tác giả của các cuốn sách Real-World Algorithms, Algorithms và Cryptography, thuộc Essential Knowledge Series của MIT Press.