Nguồn gốc của sự bất định lượng tử là gì?

Dù các thiết bị đo lường có tốt đến đâu, một số tính chất lượng tử luôn mang theo sự bất định vốn có. Chúng ta có thể tìm ra nguyên nhân tại sao không?

Sự bất định lượng tử và câu hỏi về bản chất

Có lẽ đặc tính kỳ lạ nhất mà chúng ta phát hiện ra về Vũ trụ là thực tại vật lý của chúng ta dường như không được điều hành bởi các quy luật tất định thuần túy. Thay vào đó, ở cấp độ lượng tử cơ bản, các quy luật vật lý chỉ mang tính xác suất: bạn có thể tính toán khả năng xảy ra của các kết quả thí nghiệm có thể xảy ra, nhưng chỉ khi đo lường đại lượng được đặt câu hỏi, bạn mới thực sự xác định được hệ thống cụ thể của mình đang làm gì tại thời điểm đó.

Hơn nữa, chính hành động đo lường/quan sát một số đại lượng nhất định dẫn đến sự gia tăng bất định trong một số tính chất liên quan: những gì các nhà vật lý gọi là các biến liên hợp.

Nhiều người đã đưa ra ý tưởng rằng sự bất định và tính không tất định này có thể chỉ là biểu kiến và có thể là do một số biến ẩn ẩn giấu nào đó thực sự mang tính tất định. Tuy nhiên, chúng ta vẫn chưa tìm được cơ chế nào cho phép dự đoán chính xác bất kỳ kết quả lượng tử nào.

Liệu các trường lượng tử vốn có trong không gian có phải là nguyên nhân chính? Liệu chân không lượng tử có phải là yếu tố cung cấp những gì cần thiết để gây ra sự bất định lượng tử mà chúng ta trải nghiệm mỗi khi cố gắng đo lường đồng thời những đại lượng không thể biết chính xác cùng một lúc?

Hãy cùng xem Vũ trụ nói gì về ý tưởng này.

Hiện tượng sóng – hạt

Các quỹ đạo của một hạt trong một hộp (còn được gọi là giếng vuông vô hạn) trong cơ học cổ điển (A) và cơ học lượng tử (B–F). Trong (A), hạt di chuyển với vận tốc không đổi, bật qua lại. Trong (B – F), các nghiệm hàm sóng của phương trình Schrödinger phụ thuộc thời gian được hiển thị cho cùng hình học và thế năng.

Trục ngang là vị trí, trục dọc là phần thực (màu xanh) hoặc phần ảo (màu đỏ) của hàm sóng. Các trạng thái đứng yên (B, C, D) và không đứng yên (E, F) chỉ cung cấp xác suất cho vị trí của hạt thay vì câu trả lời xác định về vị trí của nó tại một thời điểm cụ thể.

Trong vật lý lượng tử, có hai cách chính để xem xét sự bất định.

Một là Tôi tạo ra hệ thống của mình với những tính chất cụ thể này, và khi tôi quay lại sau một khoảng thời gian, tôi có thể nói gì về những tính chất đó?

Đối với một số tính chất – như khối lượng của một hạt ổn định, điện tích của một hạt, mức năng lượng của electron trong trạng thái cơ bản của nguyên tử của nó, – những tính chất này sẽ không thay đổi. Miễn là không có tương tác thêm giữa hạt lượng tử và môi trường xung quanh, các tính chất này sẽ thuộc phạm vi của những gì đã biết, không có sự bất định.

Nhưng một số tính chất khác lại ít chắc chắn hơn. Đặt một electron tự do vào không gian tại một vị trí được biết chính xác, và khi bạn quay lại sau đó, vị trí của electron không còn có thể biết chắc chắn nữa: hàm sóng mô tả vị trí của nó lan rộng theo thời gian.

Nếu bạn muốn biết một hạt không ổn định đã phân rã hay chưa, bạn chỉ có thể tìm ra bằng cách đo các tính chất của hạt đó và xem nó đã phân rã hay chưa.

Nếu bạn hỏi khối lượng của một hạt không ổn định đã phân rã phóng xạ là bao nhiêu, bạn có thể tái tạo điều này bằng cách đo năng lượng và động lượng của từng hạt mà nó đã phân rã thành. Tuy nhiên, bạn sẽ nhận được câu trả lời hơi khác nhau qua từng sự kiện, bất định phụ thuộc vào thời gian sống của hạt.

Bất định từ sự tiến hóa theo thời gian

Đây là một dạng bất định phát sinh do sự tiến hóa theo thời gian: do bản chất lượng tử của thực tại đảm bảo rằng một số tính chất chỉ có thể được biết với độ chính xác nhất định. Khi thời gian trôi qua, sự bất định đó lan rộng vào tương lai, dẫn đến một trạng thái vật lý không thể biết chính xác tùy ý.

Tuy nhiên, còn có một cách khác mà sự bất định xuất hiện: vì một số cặp đại lượng – các biến liên hợp đó – liên quan với nhau theo cách mà việc biết một biến càng chính xác sẽ làm giảm kiến thức bạn có thể có về biến còn lại.

Hiện tượng này xuất phát trực tiếp từ nguyên lý bất định Heisenberg, và nó xuất hiện trong nhiều tình huống khác nhau.

Ví dụ phổ biến nhất là giữa vị trí và động lượng. Càng đo chính xác vị trí của một hạt, bạn càng không thể biết chắc động lượng của nó – tức là tốc độ và hướng lượng chuyển động của nó.

Điều này có ý nghĩa nếu bạn nghĩ về cách thực hiện phép đo vị trí: bằng cách gây ra một tương tác lượng tử giữa hạt mà bạn đang đo với một lượng tử khác, có hoặc không có khối lượng nghỉ.

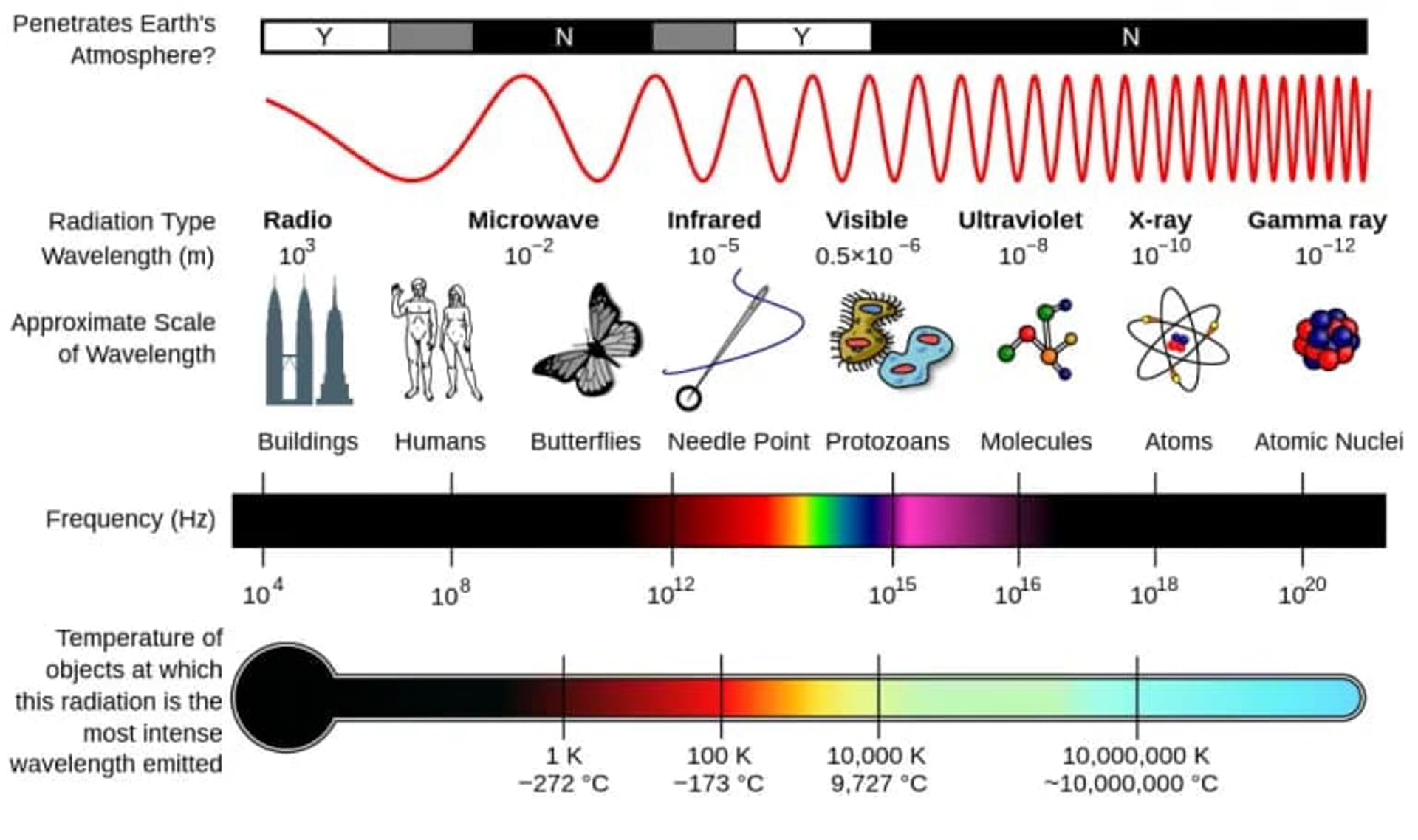
Kích thước, bước sóng và thang nhiệt độ/ năng lượng tương ứng với các phần khác nhau của phổ điện từ. Bạn cần phải tiến đến mức năng lượng cao hơn và bước sóng ngắn hơn để khảo sát các thang đo nhỏ nhất. Ánh sáng cực tím đủ để ion hóa các nguyên tử, nhưng khi Vũ trụ giãn nở, ánh sáng bị dịch chuyển hệ thống sang nhiệt độ thấp hơn và bước sóng dài hơn.

Nếu bạn kích thích một hạt lượng tử bằng cách khiến nó tương tác với một hạt lượng tử khác, sẽ xảy ra một sự trao đổi động lượng giữa chúng.

– Năng lượng của hạt tương tác càng lớn,

– Bước sóng của nó càng ngắn,

– Dẫn đến vị trí được biết chính xác hơn,

– Nhưng cũng dẫn đến sự gia tăng năng lượng và động lượng truyền cho hạt,

– Điều này dẫn đến bất định lớn hơn trong động lượng của nó.

Bạn có thể nghĩ rằng mình có thể làm điều gì đó thông minh để gian lận hiện tượng này, chẳng hạn như đo động lượng của hạt phát ra mà bạn đã sử dụng để xác định vị trí của hạt. Nhưng đáng tiếc, nỗ lực như vậy cũng không thể giúp bạn tránh khỏi bất định lượng tử.

Lượng bất định giữa hai đại lượng liên hợp

Luôn có một lượng bất định tối thiểu phải được bảo tồn: tích của bất định trong mỗi hai đại lượng liên hợp luôn lớn hơn hoặc bằng một giá trị nhất định. Dù bạn đo lường vị trí (Δx) và/hoặc động lượng (Δp) của từng hạt trong các tương tác này tốt đến đâu, tích của bất định (ΔxΔp) luôn lớn hơn hoặc bằng một nửa hằng số Planck giảm, ħ/2.

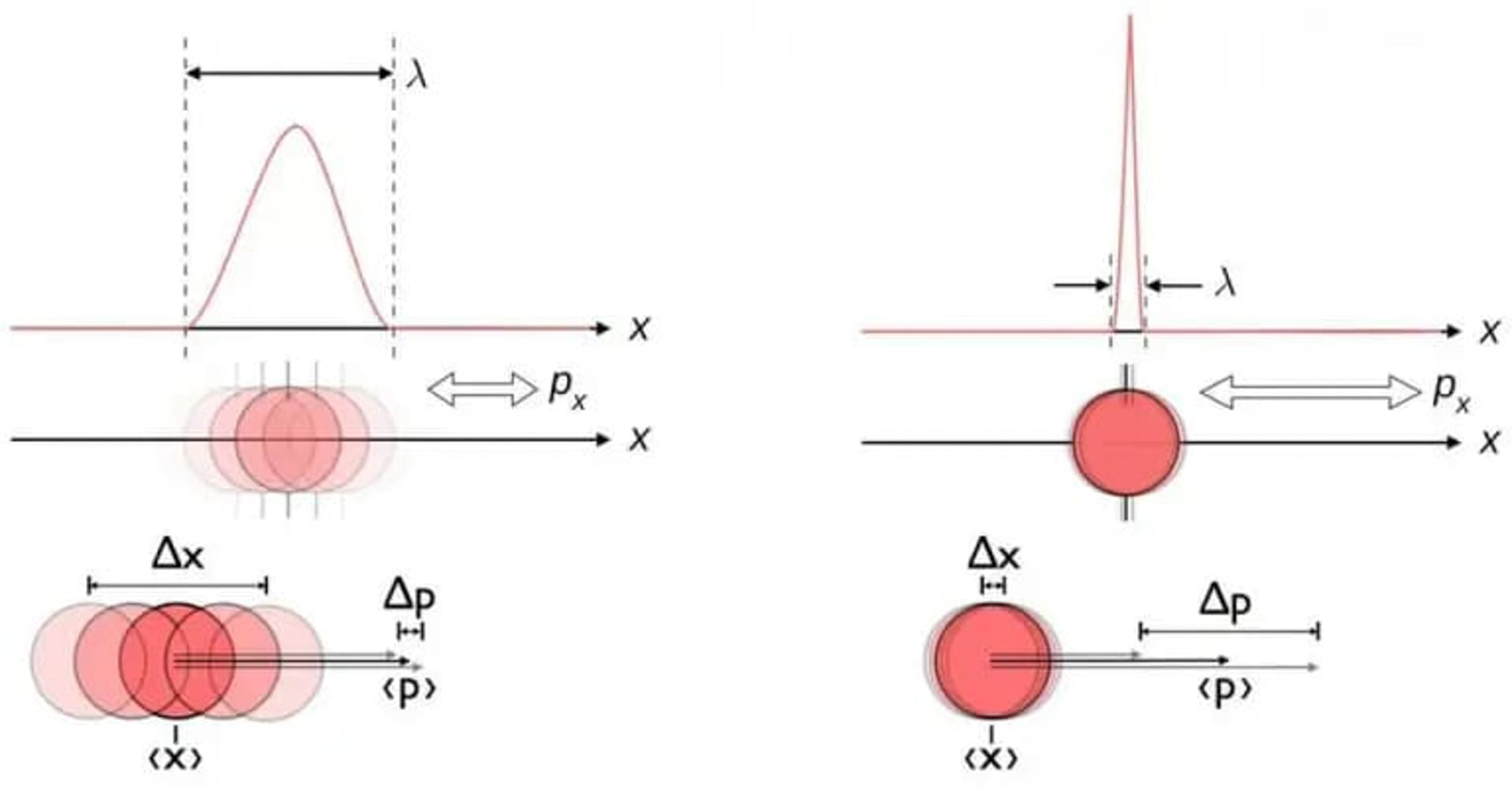
Mối quan hệ bất định nội tại giữa vị trí và động lượng. Khi một đại lượng được biết chính xác hơn, đại lượng kia sẽ khó xác định chính xác hơn. Cả vị trí và động lượng đều được mô tả tốt hơn bằng hàm sóng xác suất thay vì một giá trị duy nhất. Các cặp biến liên hợp khác, bao gồm năng lượng và thời gian, spin trong hai hướng vuông góc, hoặc vị trí góc và động lượng góc, cũng thể hiện mối quan hệ bất định tương tự.

Không chỉ vị trí và động lượng, mà nhiều đại lượng khác cũng thể hiện mối quan hệ bất định này. Chúng bao gồm:

– Hướng và động lượng góc.

– Năng lượng và thời gian.

– Spin của một hạt theo các hướng vuông góc,

– Thế điện và điện tích tự do.

– Thế từ và dòng điện tự do.

– Và nhiều đại lượng khác.

Chúng ta đang sống trong một vũ trụ lượng tử, vì vậy câu hỏi liệu có tồn tại một dạng biến ẩn nào đó đứng đằng sau những điều kỳ lạ này của lượng tử là hợp lý. Nhiều người đã suy ngẫm liệu những khái niệm lượng tử này và sự bất định không thể tránh khỏi này là thuộc tính cố hữu của tự nhiên, hay có một nguyên nhân tiềm ẩn mà chúng ta chưa thể xác định được. Cách tiếp cận sau, được nhiều nhà tư tưởng lớn trong lịch sử ủng hộ (bao gồm Einstein), thường được gọi là giả thiết biến ẩn.

Một cách dễ hình dung về biến ẩn là tưởng tượng vũ trụ, cùng tất cả các hạt trong đó, như đang nằm trên một tấm đĩa rung nhanh chóng và hỗn loạn, nhưng với biên độ nhỏ nhất. Khi quan sát vũ trụ ở các quy mô lớn, ta không thấy ảnh hưởng của sự rung động này; phông nền của vũ trụ dường như ổn định, không thay đổi, và không có dao động.

Nhưng khi bạn nhìn vào quy mô nhỏ hơn, bạn sẽ nhận ra các thuộc tính lượng tử này. Các đại lượng dao động, các hiện tượng không duy trì sự ổn định hoàn toàn theo thời gian, và khi bạn cố gắng đo lường chính xác một thuộc tính lượng tử, mức độ bất định trong đại lượng liên hợp sẽ tăng lên.

Nguồn gốc của dao động lượng tử

Dựa trên thực tế rằng có các trường lượng tử bao phủ toàn bộ không gian, thậm chí cả không gian trống rỗng, bạn có thể dễ dàng hình dung rằng chính các trường này là nguồn gốc của mọi bất định. Sự bất định mà chúng ta thấy có thể phát sinh như một hệ quả của chân không lượng tử.

Ngay cả trong không gian trống rỗng, năng lượng chân không vẫn không bằng 0. Nếu có các hạt hoặc trường bổ sung vượt ngoài dự đoán của Mô hình chuẩn, chúng sẽ ảnh hưởng đến chân không lượng tử và thay đổi các thuộc tính của nhiều đại lượng khỏi các dự đoán của Mô hình chuẩn. Tuy nhiên, đóng góp của QCD không thể tính toán một cách xấp xỉ, như cách chúng ta làm với điện từ học.

Đây chắc chắn không phải một ý tưởng dễ bác bỏ, bởi thực tế là sự bất định lượng tử đã ăn sâu vào cách hiểu cơ bản của chúng ta về các hạt và trường. Mọi công thức (hoạt động hiệu quả) của cơ học lượng tử và lý thuyết trường lượng tử đều bao gồm nó, và bao gồm ở mức độ cơ bản, không chỉ như một bổ sung sau này. Thực tế, chúng ta thậm chí không biết cách sử dụng lý thuyết trường lượng tử để tính toán đóng góp tổng thể vào chân không lượng tử cho mỗi lực cơ bản; chúng ta chỉ biết, thông qua đo lường năng lượng tối, tổng đóng góp này phải như thế nào. Khi cố gắng thực hiện các tính toán đó, kết quả chúng ta nhận được thường phi lý, không cung cấp bất kỳ thông tin ý nghĩa nào.

Tuy nhiên, có một số thông tin khó giải thích nếu cho rằng dao động trong chính không gian là nguyên nhân gây ra bất định lượng tử và sự lan truyền của gói sóng mà chúng ta quan sát. Thí dụ, hãy xem xét điều gì xảy ra khi bạn lấy một hạt lượng tử có mô men góc nội tại (spin), để nó di chuyển qua không gian, và áp dụng một từ trường lên nó.

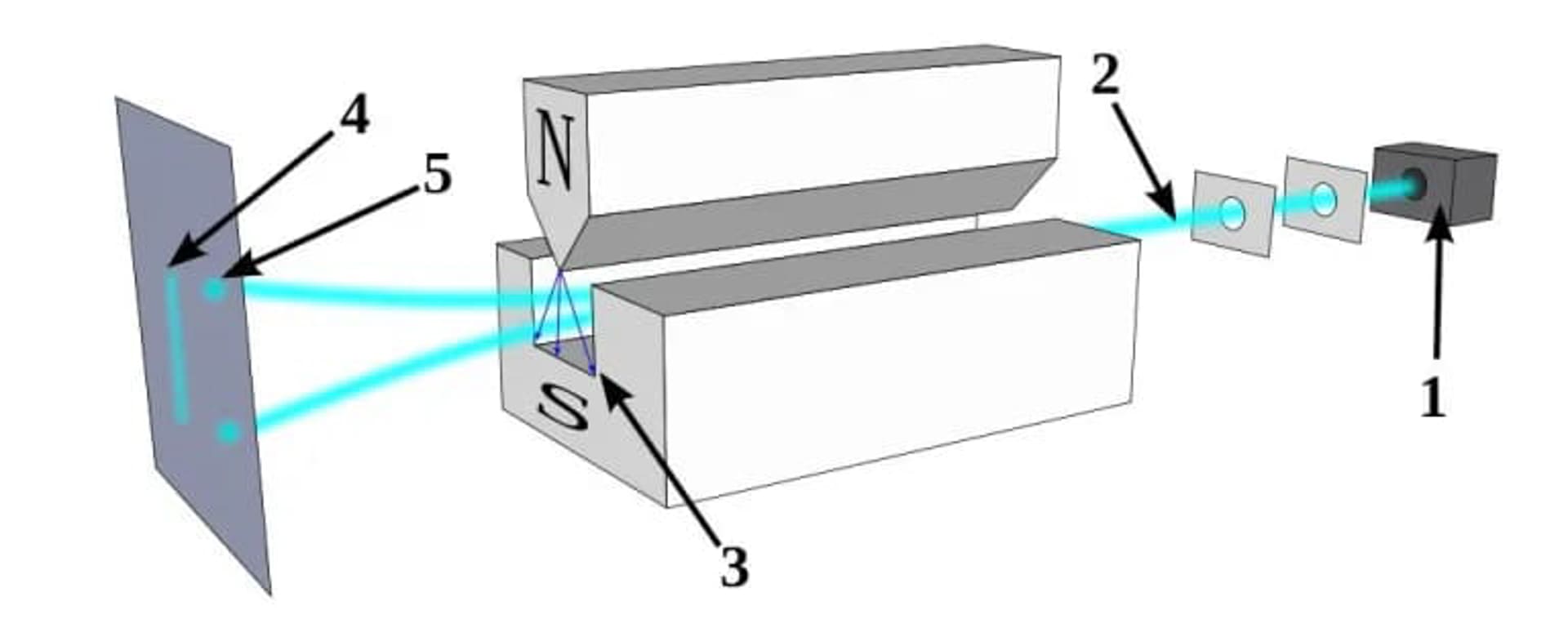
Trong thí nghiệm Stern – Gerlach, minh họa ở đây, một hạt lượng tử với spin hữu hạn được đưa qua từ trường. Điều này làm cho spin của hạt trở nên xác định rõ theo hướng của từ trường: hoặc là dương (spin hướng lên) hoặc là âm (spin hướng xuống). Mỗi hạt sẽ đi theo một trong hai đường và sau đó không còn bất định về spin của nó theo trục của từ trường đã áp dụng. Kết quả thu được là một tập hợp các giá trị rời rạc (5), thay vì một phổ liên tục các giá trị (4) như bạn có thể mong đợi nếu spin được định hướng ngẫu nhiên trong không gian ba chiều.

Hạt đó sẽ lệch đi một lượng dương hoặc âm, phụ thuộc vào hướng của từ trường bạn áp dụng và hướng spin của hạt (dương hoặc âm). Sự lệch hướng xảy ra dọc theo cùng chiều mà từ trường được áp dụng.

Giờ đây, hãy áp dụng một từ trường theo một hướng khác, vuông góc với hướng ban đầu. Bạn đã xác định được spin theo một hướng cụ thể, vậy điều gì sẽ xảy ra nếu áp dụng từ trường theo một hướng khác?

Câu trả lời là hạt sẽ lệch một lần nữa, với xác suất 50/50: hoặc hướng thẳng hàng với từ trường hoặc ngược hướng với từ trường.

Nhưng đây chưa phải là phần thú vị nhất. Điều thú vị là hành động đo lường này, việc áp dụng từ trường bổ sung theo hướng vuông góc, thực sự phá hủy thông tin mà bạn đã có từ việc áp dụng từ trường đầu tiên. Nếu bạn áp dụng lại từ trường giống như đã làm ở phần đầu thí nghiệm, các hạt – dù trước đó đã hướng dương – giờ đây sẽ có spin ngẫu nhiên: 50/50 thẳng hàng hoặc ngược hướng với từ trường.

Khi một hạt có spin lượng tử đi qua một nam châm định hướng, nó sẽ chia tách theo ít nhất hai hướng, phụ thuộc vào hướng spin. Nếu có một nam châm khác được lắp cùng hướng, không có sự phân tách nào thêm xảy ra. Tuy nhiên, nếu có một nam châm thứ ba được chèn vào giữa hai nam châm theo hướng vuông góc, không chỉ các hạt chia tách theo hướng mới, mà thông tin về hướng ban đầu bị phá hủy, làm cho các hạt chia tách một lần nữa khi đi qua nam châm cuối cùng.

Không gian trống có chịu trách nhiệm cho sự bất định?

Rất khó để giải thích hiện tượng này nếu giả định rằng chính chân không lượng tử là nguyên nhân gây ra toàn bộ sự bất định lượng tử. Trong trường hợp này, hành vi của hạt phụ thuộc vào từ trường bên ngoài mà bạn áp dụng và các tương tác sau đó mà hạt trải qua, chứ không phải vào các thuộc tính của không gian trống mà hạt đi qua.

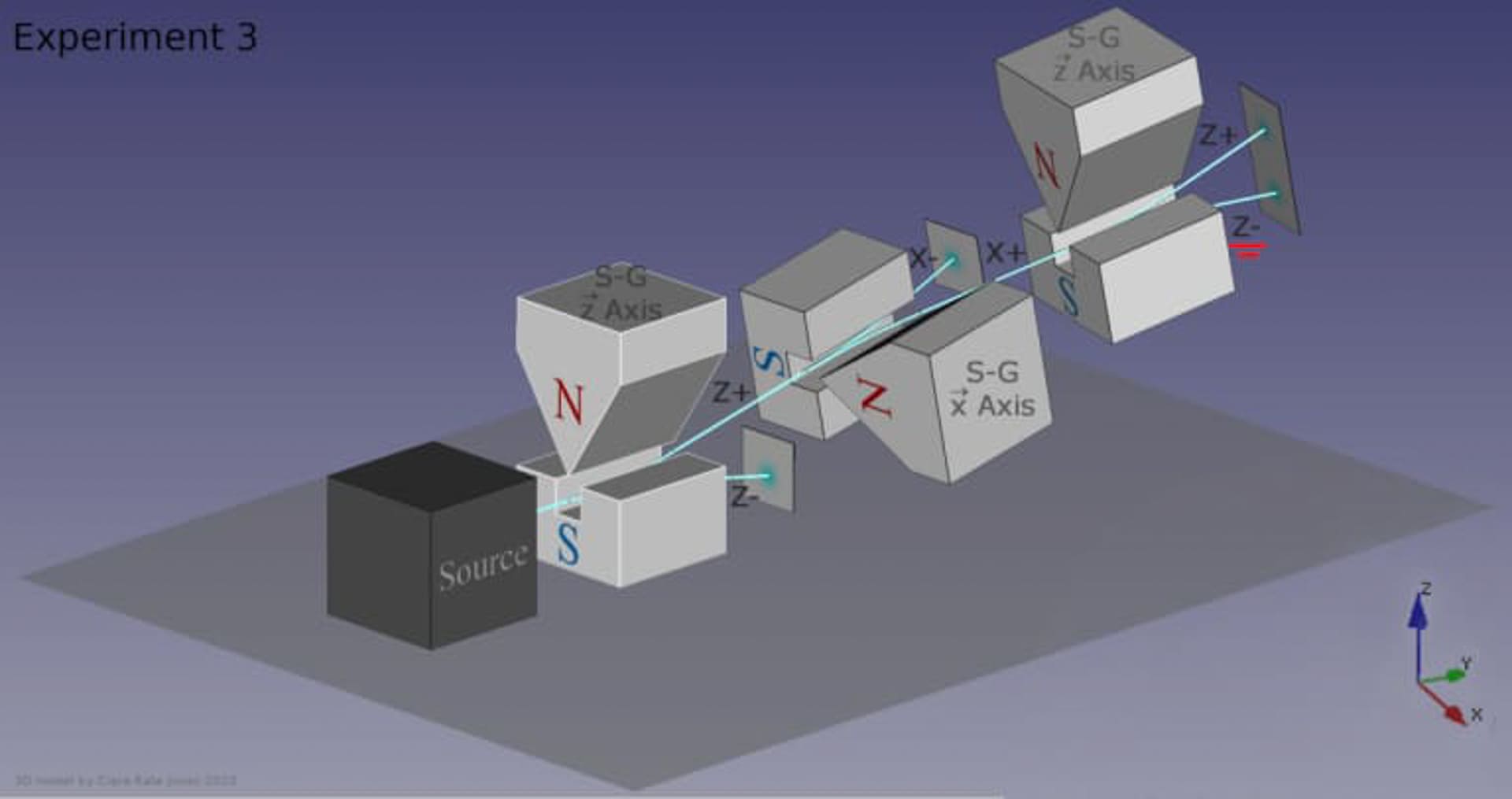
Nếu bạn loại bỏ nam châm thứ hai (nam châm định hướng vuông góc với hai nam châm còn lại), sẽ không có sự bất định nào về spin của hạt khi nó đến được nam châm thứ ba.

Khó có thể hình dung cách không gian trống hoặc chân không lượng tử có thể chịu trách nhiệm cho sự bất định lượng tử dựa trên kết quả của thí nghiệm này. Chính các tương tác (hoặc thiếu vắng tương tác) mà hệ lượng tử trải qua mới quyết định cách sự bất định lượng tử biểu hiện, chứ không phải thuộc tính nội tại nào đó của các trường bao phủ toàn bộ không gian.

Dù muốn hay không, thực tế của những gì bạn quan sát được phụ thuộc vào cách và việc bạn quan sát nó; các kết quả thí nghiệm sẽ khác nhau tùy thuộc vào cấu hình cụ thể của thiết bị đo lường.

Electron thể hiện các tính chất sóng cũng như hạt và có thể được sử dụng để tạo ảnh hoặc kiểm tra kích thước hạt giống như ánh sáng. Ở đây, bạn có thể thấy kết quả của một thí nghiệm nơi các electron được bắn từng cái một qua một khe đôi. Khi đủ số lượng electron được bắn qua, mô hình giao thoa sẽ hiện rõ.

Cho đến nay, không có lý thuyết nào về các biến ẩn đưa ra được bằng chứng thực nghiệm hoặc quan sát rằng có một thực tại khách quan nằm ngoài sự đo lường của chúng ta. Nhiều người tin rằng điều này là đúng, nhưng đó chỉ dựa trên trực giác và lập luận triết học – không phải là lý do khoa học hợp lệ để đưa ra bất kỳ kết luận nào.

Điều đó không có nghĩa là con người không nên tiếp tục xây dựng các lý thuyết như vậy hoặc cố gắng thiết kế các thí nghiệm để phát hiện hoặc bác bỏ sự tồn tại của các biến ẩn. Đó là một phần của cách khoa học tiến lên phía trước. Nhưng cho đến nay, tất cả các công thức đó chỉ dẫn đến những ràng buộc và sự bác bỏ các lớp lý thuyết biến ẩn cụ thể. Ý tưởng rằng các biến ẩn tồn tại và chúng được mã hóa trong chân không lượng tử không thể bị bác bỏ.

Nhưng nếu tôi phải đặt cược vào nơi cần tìm tiếp theo, tôi sẽ lưu ý rằng trong lý thuyết hấp dẫn (Newtonian), cũng có các biến liên hợp: thế năng hấp dẫn và mật độ khối lượng. Nếu mối liên hệ với điện từ học (giữa thế điện và điện tích tự do) vẫn đúng, như chúng ta kỳ vọng, thì điều đó có nghĩa là chúng ta có thể trích xuất một mối quan hệ bất định cho lực hấp dẫn.

Liệu lực hấp dẫn có phải là một lực lượng lượng tử cố hữu? Một ngày nào đó, chúng ta có thể xác định thực nghiệm xem sự bất định lượng tử có tồn tại cho lực hấp dẫn hay không. Nếu có, chúng ta sẽ có câu trả lời.